“中国式过马路”存在很大的交通安全隐患.某调查机构为了解路人对“中国式过马路 ”的态度是否与性别有关,从马路旁随机抽取 名路人进行了问卷调查,得到了如下列联表:
名路人进行了问卷调查,得到了如下列联表:
| |
男性 |
女性 |
合计 |
| 反感 |
10 |
|
|
| 不反感 |
|
8 |
|
| 合计 |
|
|
30 |
已知在这 人中随机抽取
人中随机抽取 人抽到反感“中国式过马路 ”的路人的概率是
人抽到反感“中国式过马路 ”的路人的概率是 .
.
(Ⅰ)请将上面的列联表补充完整(在答题卷上直接填写结果,不需要写求解过程),并据此资料判断是否有95%的把握认为反感“中国式过马路 ”与性别有关?
(Ⅱ)若从这 人中的女性路人中随机抽取
人中的女性路人中随机抽取 人参加一活动,记反感“中国式过马路”的人数为
人参加一活动,记反感“中国式过马路”的人数为 ,求
,求 的分布列.
的分布列.
附: ,其中
,其中 
 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
已知 (I)若a=3,求
(I)若a=3,求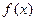 的单调区间和极值;(II)已知
的单调区间和极值;(II)已知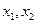 是
是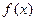 的两个不同的极值点,且
的两个不同的极值点,且 ,若
,若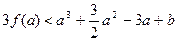 恒成立,求实数
恒成立,求实数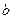 的取值范围.
的取值范围.
设函数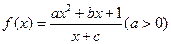 为奇函数,且
为奇函数,且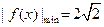 ,数列
,数列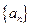 与
与 满足如下关系:
满足如下关系: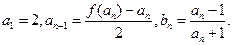 (1)求
(1)求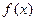 的解析式;(2)求数列
的解析式;(2)求数列 的通项公式
的通项公式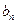 ;(3)记
;(3)记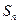 为数列
为数列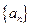 的前
的前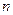 项和,求证:对任意的
项和,求证:对任意的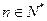 有
有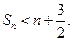
在△ABC中, .(I)求∠C的大小;(Ⅱ)设角A,B,C的对边依次为
.(I)求∠C的大小;(Ⅱ)设角A,B,C的对边依次为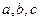 ,若
,若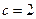 ,且△ABC是锐角三角形,求
,且△ABC是锐角三角形,求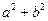 的取值范围.
的取值范围.
已知: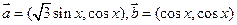 ,
,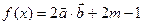 (
( ).(Ⅰ) 求
).(Ⅰ) 求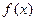 关于
关于 的表达式,并求
的表达式,并求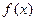 的最小正周期;(Ⅱ) 若
的最小正周期;(Ⅱ) 若 时,
时,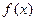 的最小值为5,求
的最小值为5,求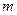 的值.
的值.
( 12分)近段时间我国北方严重缺水, 某城市曾一度取消洗车行业. 时间久了,车容影响了市容市貌. 今年该市决定引进一种高科技产品污水净化器,允许洗车行开始营业,规定洗车行必须购买这种污水净化器,使用净化后的污水(达到生活用水标准)洗车. 污水净化器的价格是每台90万元,全市统一洗车价格为每辆每次8元. 该市今年的汽车总量是80000辆,预计今后每年汽车数量将增加2000辆.洗车行A经过测算,如果全市的汽车总量是x,那么一年内在该洗车行洗车的平均辆次是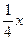 ,该洗车行每年的其他费用是20000元. 问:洗车行A从今年开始至少经过多少年才能收回购买净化器的成本?(注:洗车行A买一台污水净化器就能满足洗车净水需求)
,该洗车行每年的其他费用是20000元. 问:洗车行A从今年开始至少经过多少年才能收回购买净化器的成本?(注:洗车行A买一台污水净化器就能满足洗车净水需求)