某市芙蓉社区为了解家庭月均用水量（单位：吨），从社区中随机抽查100户，获得每户2013年3月的用水量，并制作了频率分布表和频率分布直方图（如图）.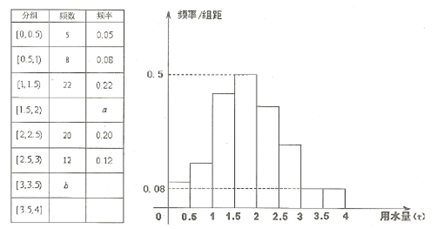
(Ⅰ)分别求出频率分布表中a、b的值，并估计社区内家庭月用水量不超过3吨的频率；
(Ⅱ）设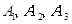
是月用水量为[0，2)的家庭代表.
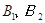是月用水量为[2，4]的家庭代表.若从这五位代表中任选两人参加水价听证会，请列举出所有不同的选法，并求家庭代表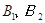至少有一人被选中的概率.
某项竞赛分别为初赛、复
赛、决赛三个阶段进行，每个阶段选手要
回答一个问题.规定正确回答问题者进入下一阶段竞赛，否则即遭淘汰.已知某选手通过初赛、复赛、决赛的概率分别是
，且各阶段通过与否相互独立.
（1）求该选手在复赛阶段被淘汰的概率；
（2）设该选手在竞赛中回答问题的个数为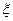
，求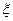的分布列、数学期望和方差.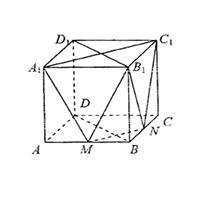
已知
，且
．
（1）求实数
的值；
（2）求函数
的最大值和最小值．
（本小题满分12分）
直三棱柱ABO-A1B1O1中，∠AOB=90°，D为AB的中点，AO=BO=BB1=2.
①求证：BO1⊥AB1；
②求证：BO1∥平面OA1D；
③求三棱锥B—A1OD的体积。
（本小题满分12分）
甲、乙两人独立地破译一份密码，甲能破译出密码的概率是1/3，乙能破译出密码的概率是1/4，试求：
①甲、乙两人都译不出密码的概率；
②甲、乙两人中恰有一人能译出密码的概率；
③甲、乙两人中至多有一人能译出密码的概率.
（本小题满分12分）
四面体ABCD中，对棱AD⊥BC，对棱AB⊥CD，试证明：AC⊥BD.