如图1，在△ABC中，∠ACB90°，ACBC，直线MN经过-优题课

如图1，在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E。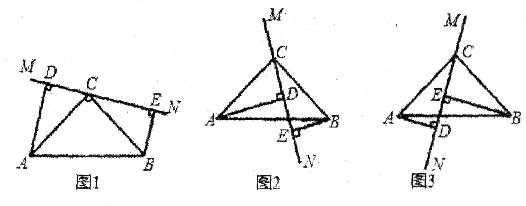

（1）①写出图1中的一对全等三角形；②写出图1中线段DE、AD、BE所具有的等量关系；（不必说明理由）
（2）当直线MN绕点C旋转到图2的位置时，请说明DE=AD－BE的理由；
（3）当直线MN绕点C旋转到图3的位置时，试问DE、AD、BE又具有怎样的等量关系?请直接写出这个等量关系（不必说明理由）。

科目数学题型解答题难度中等

知识点：三角形的五心

已知关于 $x$ 的一元二次方程 $x^{2} + （ 2 k + 1 ） x + k^{2} + 1 ＝ 0$ 有两个不等实数根 $x_{1} ， x_{2}$ ．

（1）求 $k$ 的取值范围；

（2）若 $x_{1} x_{2} ＝ 5$ ，求 $k$ 的值．

解分式方程： $\frac{1}{x} = \frac{4}{x + 3}$ ．

如图，抛物线 $y ＝ ﹣ x^{2} + 3 x + 4$ 与 $x$ 轴交于 $A ， B$ 两点（点 $A$ 位于点 $B$ 的左侧），与 $y$ 轴交于 $C$ 点，抛物线的对称轴 $l$ 与 $x$ 轴交于点 $N$ ，长为 $1$ 的线段 $P Q$ （点 $P$ 位于点 $Q$ 的上方）在 $x$ 轴上方的抛物线对称轴上运动．

（1）直接写出 $A ， B ， C$ 三点的坐标；

（2）求 $C P + P Q + Q B$ 的最小值；

（3）过点 $P$ 作 $P M ⊥ y$ 轴于点 $M$ ，当 $△ C P M$ 和 $△ Q B N$ 相似时，求点 $Q$ 的坐标．

如图， $A B$ 是 $⊙ O$ 的直径，点 $C$ 是圆上的一点， $C D ⊥ A D$ 于点 $D$ ， $A D$ 交 $⊙ O$ 于点 $F$ ，连接 $A C$ ，若 $A C$ 平分 $∠ D A B$ ，过点 $F$ 作 $F G ⊥ A B$ 于点 $G$ 交 $A C$ 于点 $H$ ．

（1）求证： $C D$ 是 $⊙ O$ 的切线；

（2）延长 $A B$ 和 $D C$ 交于点 $E$ ，若 $A E ＝ 4 B E$ ，求 $\cos ∠ D A B$ 的值；

（3）在（2）的条件下，求 $\frac{FH}{AF}$ 的值．

今年，某市举办了一届主题为“强国复兴有我”的中小学课本剧比赛．某队伍为参赛需租用一批服装，经了解，在甲商店租用服装比在乙商店租用服装每套多 $10$ 元，用 $500$ 元在甲商店租用服装的数量与用 $400$ 元在乙商店租用服装的数量相等．

（1）求在甲，乙两个商店租用的服装每套各多少元？

（2）若租用 $10$ 套以上服装，甲商店给以每套九折优惠．该参赛队伍准备租用 $20$ 套服装，请问在哪家商店租用服装的费用较少，并说明理由．

试卷网试题网古诗词网作文网范文网