小明遇到这样一个问题:如图1,在边长为 的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ的面积。小明发现:分别延长QE,MF,NG,PH,交FA,GB,HC,ED的延长线于点R,S,T,W,可得△RQF,△SMG,△TNH,△WPE是四个全等的等腰直角三角形(如图2)请回答:
的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ的面积。小明发现:分别延长QE,MF,NG,PH,交FA,GB,HC,ED的延长线于点R,S,T,W,可得△RQF,△SMG,△TNH,△WPE是四个全等的等腰直角三角形(如图2)请回答:
(1)若将上述四个等腰直角三角形拼成一个新的正方形(无缝隙,不重叠),则这个新的正方形的边长为 ;
(2)求正方形MNPQ的面积。参考小明思考问题的方法,解决问题:
(3)如图3,在等边△ABC各边上分别截取AD=BE=CF,再分别过点D,E,F作BC,AC,AB的垂线,得到等边△RPQ,若 ,则AD的长为 。
,则AD的长为 。
如图,⊙O是△ABC的外接圆,AB=AC,P是⊙O上一点.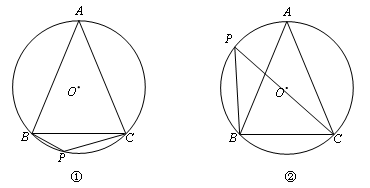
(1)请你只用无刻度的直尺,分别画出图①和图②中∠P的平分线;
(2)结合图②,说明你这样画的理由.
近期,中国足球改革方案由中央深改小组审议通过,中国足球迎来春天的气息.甲、乙、丙三人进行踢足球训练.球从一个人脚下随机传到另外一个人脚下,共传球三次.
(1)若开始时球在甲脚下,求经过三次传球后,球传回甲脚下的概率是多少?
(2)若乙想使球经过三次传递后,球落在自己脚下的概率最大,乙会让球开始时在谁脚下?请说明理由.
城南中学九年级共有12个班,每班48名学生,学校要对该年级学生数学学科学业水平测试成绩进行抽样分析,请按要求回答下列问题:
收集数据
(1)若要从全年级学生中抽取一个48人的样本,你认为以下抽样方法中比较合理的有.①随机抽取一个班级的48名学生;②在全年级学生中随机抽取48名学生;③在全年级12个班中分别各随机抽取4名学生.
整理数据
(2)将抽取的48名学生的成绩进行分组,绘制出的频数分布表和成绩分布扇形统计图如下.请根据图表中数据填空:
①C类和D类部分的圆心角度数分别为;;
②估计全年级A、B类学生大约一共有名.
| 成绩(单位:分) |
频数 |
频率 |
| A类(80~100) |
24 |
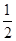 |
| B类(60~79) |
12 |
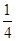 |
| C类(40~59) |
8 |
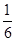 |
| D类(0~39) |
4 |
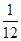 |
分析数据
(3)教育主管部门为了解学校教学情况,将同层次的城南、城北两所中学的抽样数据进行对比,得下表:
| 学校 |
平均数 |
极 差 |
方 差 |
A、B类的频率和 |
| 城南中学 |
71 |
52 |
432 |
0.75 |
| 城北中学 |
71 |
80 |
497 |
0.82 |
你认为哪所学校的教学效果较好?结合数据,请提出一个解释来支持你的观点.
如图,A、D、F、B在同一直线上,AE=BC,且AE∥BC,AD=BF.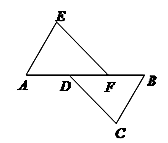
(1)求证: ;
;
(2)连ED,CF,则四边形EDCF是.(从平行四边形,矩形,菱形,正方形中选填).
(1)计算:
(2)先化简,再求值: ,请代入一个你喜欢的值并进行计算.
,请代入一个你喜欢的值并进行计算.