如图,A、D、F、B在同一直线上,AE=BC,且AE∥BC,AD=BF.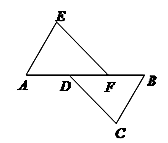
(1)求证: ;
;
(2)连ED,CF,则四边形EDCF是 .(从平行四边形,矩形,菱形,正方形中选填).
如图,已知矩形ABCD中,AB=10,AD=4,点E为CD边上的一个动点,连结AE、BE,以AE为直径作圆,交AB于点F,过点F作FH⊥BE于H,直线FH交⊙O于点G.
(1)求证:⊙O必经过点D;
(2)若点E运动到CD的中点,试证明:此时FH为⊙O的切线;
(3)当点E运动到某处时,AE∥FH,求此时GF的长.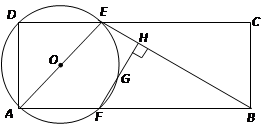
如图,已知一次函数y1 = k1x + 6与反比例函数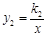 (x>0)的图象交于点A、B,且A、B两点的横坐标分别为2和4.
(x>0)的图象交于点A、B,且A、B两点的横坐标分别为2和4.
(1)k1=,k2=;
(2)求点A、B、O所构成的三角形的面积;
(3)对于x>0,试探索y1与y2的大小关系(直接写出结果).
智能手机如果安装了一款测量软件“Smart Measure”后,就可以测量物高、宽度和面积等.如图,打开软件后将手机摄像头的屏幕准星对准脚部按键,再对准头部按键,即可测量出人体的高度.其数学原理如图②所示,测量者AB与被测量者CD都垂直于地面BC.
(1)若手机显示AC = 1m,AD = 1.8m,∠CAD = 60°,求此时CD的高.(结果保留根号)
(2)对于一般情况,试探索手机设定的测量高度的公式:设AC= a,AD= b,∠CAD= α,即用a、b、α来表示CD.(提示:sin2α+ cos2α= 1)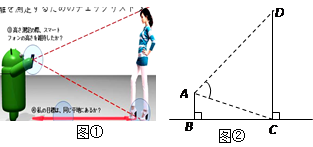
我们在配平化学方程式时,对于某些简单的方程式可以用观察法配平,对于某些复杂的方程式,还可以尝试运用方程的思想和比例的方法.例如方程式: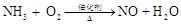 ,可以设NH3的系数为1,其余三项系数分别为x、y、z,即:
,可以设NH3的系数为1,其余三项系数分别为x、y、z,即: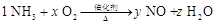 ,依据反应前后各元素守恒,得:
,依据反应前后各元素守恒,得: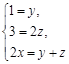 ,解之得四项系数之比为1:
,解之得四项系数之比为1: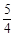 :1:
:1: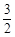 ,扩大4倍得整数比为4:5:4:6,即配平结果为
,扩大4倍得整数比为4:5:4:6,即配平结果为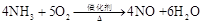 .请运用上述方法,配平化学方程式:
.请运用上述方法,配平化学方程式: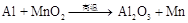 .
.
太仓人杰地灵,为了了解学生对家乡历史文化名人的知晓情况,某校对部分学生进行了随机抽样调查,并将调查结果绘制成如图所示统计图的一部分.
根据统计图中的信息,回答下列问题:
(1)本次抽样调查的样本容量是 _;
(2)在扇形统计图中,“了解很少”所在扇形的圆心角是 度;
(3)若全校共有学生1300人,那么该校约有多少名学生“基本了解”太仓的历史文化名人?