城南中学九年级共有12个班，每班48名学生，学校要对该年级学生数学学科学业水平测试成绩进行抽样分析，请按要求回答下列问题：
收集数据
（1）若要从全年级学生中抽取一个48人的样本，你认为以下抽样方法中比较合理的有 ．①随机抽取一个班级的48名学生；②在全年级学生中随机抽取48名学生；③在全年级12个班中分别各随机抽取4名学生．
整理数据
（2）将抽取的48名学生的成绩进行分组，绘制出的频数分布表和成绩分布扇形统计图如下．请根据图表中数据填空：
①C类和D类部分的圆心角度数分别为 ； ；
②估计全年级A、B类学生大约一共有 名．
| 成绩（单位：分） |
频数 |
频率 |
| A类（80～100） |
24 |
 |
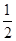| B类（60～79） |
12 |
 |
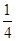| C类（40～59） |
8 |
 |
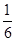| D类（0～39） |
4 |
 |
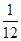分析数据
（3）教育主管部门为了解学校教学情况，将同层次的城南、城北两所中学的抽样数据进行对比，得下表：
| 学 校 |
平均数 |
极 差 |
方 差 |
A、B类的频率和 |
| 城南中学 |
71 |
52 |
432 |
0．75 |
| 城北中学 |
71 |
80 |
497 |
0．82 |
你认为哪所学校的教学效果较好？结合数据，请提出一个解释来支持你的观点．
解方程： 
计算
（1）
(2)
如图，抛物线经过点A(4，0)、B（1，0)、C（0，－2）三点．求此抛物线的解析式；
如图，在平面直角坐标系xOy中，顶点为M的抛物线y＝ax2＋bx（a＞0）经过点A和x轴正半轴上的点B，AO＝BO＝2，∠AOB＝120°．
（1）求这条抛物线的表达式；
（2）连结OM，求∠AOM的大小；
（3）如果点C在x轴上，且△ABC与△AOM相似，求点C的坐标．
如图，在平面直角坐标系中，A是抛物线
上的一个动点，且点A在第一象限内．AE⊥y轴于点E，点B坐标为（0，2），直线AB交
轴于点C，点D与点C关于y轴对称，直线DE与AB相交于点F，连结BD．设线段AE的长为m，△BED的面积为S．
（1）当
时，求S的值．
（2）求S关于
的函数解析式．
（3）①若S＝
时，求
的值；
②当m＞2时，设
，猜想k与m的数量关系并证明．