对于平面直角坐标系xOy中的点P和⊙C,给出如下定义:若⊙C上存在两个点A,B,使得∠APB=60°,则称P为⊙C 的关联点。已知点D( ,
, ),E(0,-2),F(
),E(0,-2),F( ,0)
,0)
(1)当⊙O的半径为1时,
①在点D,E,F中,⊙O的关联点是 ;
②过点F作直线交y轴正半轴于点G,使∠GFO=30°,若直线上的点P(m,n)是⊙O的关联点,求m的取值范围;
(2)若线段EF上的所有点都是某个圆的关联点,求这个圆的半径r的取值范围。
在如图所示的直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标是(﹣3,﹣1).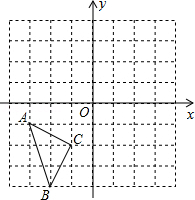
(1)将△ABC沿y轴正方向平移3个单位得到△A1B1C1,画出△A1B1C1,并写出点B1坐标;
(2)画出△A1B1C1关于y轴对称的△A2B2C2,并写出点C2的坐标.
已知:在直角坐标平面内,△ABC三个顶点的坐标分别为A(0,3),B(3,4),C(2,2)(正方形网格中每个小正方形的边长是一个单位长度)
(1)在备用图(1)中,画出△ABC向下平移4个单位长度得到△A B
B C
C ,点C
,点C 的坐标是________.
的坐标是________.
(2)在备用图(2)中,以点B为位似中心,在网格内画出△A B
B C
C ,使△A
,使△A B
B C
C 与△ABC位似,且位似比为2︰1,点C
与△ABC位似,且位似比为2︰1,点C 的坐标是________.
的坐标是________.
(3)△A B
B C
C 的面积是________平方单位.
的面积是________平方单位.
如图,已知,在△ABC中,CA=CB,∠ACB=90°,E,F分别是CA,CB边的三等分点,将△ECF绕点C逆时针旋转α角(0°<α<90°),得到△MCN,连接AM,BN.
(1)求证:AM=BN;
(2)当MA∥CN时,试求旋转角α的余弦值.
如图,在△ABC中,AB=AC,∠DAC是△ABC的一个外角.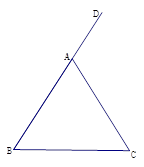
实践与操作:
根据要求尺规作图,并在图中标明相应字母(保留作图痕迹,不写作法).
(1)作∠DAC的平分线AM;
(2)作线段AC的垂直平分线,与AM交于点F,与BC边交于点E,连接AE、CF.
猜想并证明:
判断四边形AECF的形状并加以证明.
如图,在△ABC中,AB=4cm,AC=6cm.
(1)作图:作BC边的垂直平分线分别交与AC,BC于点D,E(用尺规作图法,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,连结BD,求△ABD的周长.