如图，在平面直角坐标系中，四边形ABCO是梯形，其中A（6，0），B（3，
），C（1，），动点P从点O以每秒2个单位的速度向点A运动，动点Q也同时从点B沿B→ C→O的线路以每秒1个单位的速度向点O运动，当点P到达A点时，点Q也随之停止，设点P、Q运动的时间为t（秒）.
（1）求经过A、B、C三点的抛物线的解析式；
（2）当点Q在CO边上运动时，求△OPQ的面积S与时间t的函数关系式；
（3）以O、P、Q为顶点的三角形能构成直角三角形吗？若能，请求出t的值，若不能，请说明理由；
（4）经过A、B、C三点的抛物线的对称轴、直线OB和PQ能够交于一点吗？若能，请求出此时t的值（或范围），若不能，请说明理由.
在下列网格图中，每个小正方形的边长均为1个单位．在Rt△ABC中，∠C=90°，AC=3，BC=4．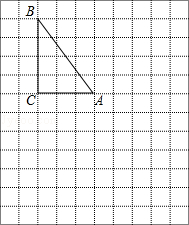
（1）试在图中做出△ABC以A为旋转中心，沿顺时针方向旋转90°后的图形△AB1C1；
（2）若点B的坐标为（﹣3，5），试在图中画出直角坐标系，并标出A、C两点的坐标；
（3）根据（2）的坐标系作出与△ABC关于原点对称的图形△A2B2C2，并标出B2、C2两点的坐标．
八（2）班组织了一次经典朗读比赛，甲、乙两队各10人的比赛成绩如下表（10分制）：
| 甲 |
7 |
8 |
9 |
7 |
10 |
10 |
9 |
10 |
10 |
10 |
| 乙 |
10 |
8 |
7 |
9 |
8 |
10 |
10 |
9 |
10 |
9 |
（1）甲队成绩的中位数是 分，乙队成绩的众数是_____分；
（2）计算乙队的平均成绩和方差；
（3）已知甲队成绩的方差是1．4分2，则成绩较为整齐的是 队．
（1）先化简，再求值：（a+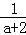
）÷（a﹣2+
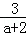），其中a=2
（2）解分式方程：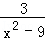
+
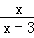=1．
AB是⊙O的直径，AD与⊙O相交，点C是⊙O上一点，经过点C的直线交AD于点E．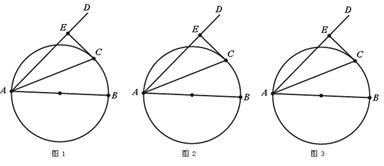
（1）如图1 ，若AC平分∠BAD，CE⊥AD于点E，求证：CE是⊙O的切线；
（2）如图2，若CE是⊙O的切线，CE⊥AD于点E，AC是∠BAD的平分线吗？说明理由；
（3）如图3，若CE是⊙O的切线，AC平分∠BAD，AB=8，AC=6，求AE的长度．
已知关于x的一元二次方程k
－（4k+1）x+3k+3=0．
（1）试说明：无论k取何值，方程总有两个实数根；
（2）若△ABC的两边AB、AC的长是方程的两个实数根，第三边BC的长为5．当△ABC是等腰三角形时，求k的值．