某商场促销方案规定：商场内所有商品案标价的80%出售，同时，当顾客在商场内消费满一定金额后，按下表获得相应的返还金额。
| 消费金额(元) |
300～400 |
400～500 |
500～600 |
600～700 |
700～900 |
… |
| 返还金额(元) |
30 |
60 |
100 |
130 |
150 |
… |
注：300~400表示消费金额大于300元且小于或等于400元，其他类同。
根据上述促销方案，顾客在该商场购物可以获得双重优惠。例如，若购买标价为400元的商品，则消费金额为320元，获得的优惠额为400´(1-80%)+30=110(元)。
（1）购买一件标价为1000元的商品，顾客获得的优惠额是多少？
（2）如果顾客购买标价不超过800元的商品，要使获得的优惠额不少于226元，那么该商品的标价至少为多少元？
如图，已知AB//CD，∠BAE=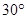
，∠DCE=
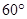，EF、EG三等分∠AEC（即∠AEF=∠FEG=∠GEC）．
（1）求∠AEF的度数；（2）EF//AB吗？为什么？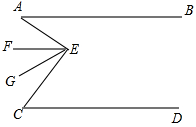
现有足够多除颜色外均相同的球，请你从中选12个球设计摸球游戏．
（1）使摸到红球的概率和摸到白球的概率相等；
（2）使摸到红球、白球、黑球的概率都相等；
（3）使摸到红球的概率和摸到白球的概率相等，且都小于摸到黑球的概率．
为推进阳光体育活动的开展，某校九年级三班同学组建了足球、篮球、乒乓球、跳绳四个体育活动小组．经调查全班同学全员参与，各活动小组人数分布情况的扇形图和条形图如下：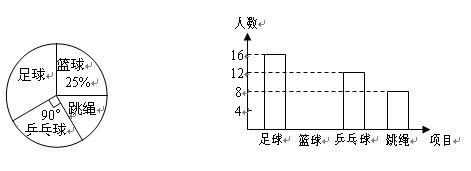
（1）求该班学生人数；
（2）请你补上条形图的空缺部分；
（3）求跳绳人数所占扇形圆心角的大小．
在下列图形中，补充作图：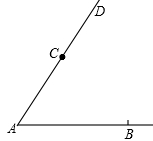
（1）在AD的右侧作∠DCP＝∠DAB（尺规作图，不写作法，保留作图痕迹）；
（2）CP与AB会平行吗？为什么？
计算：(1)（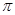
－3）0+（－0.125）2012×82012
(2)（3m3n2）2（－2m2）3（－n3）4
(3)（66x6y3－24x4y2+9x2y）÷（－3x2y）
(4)（2x+3y）（2x－3y）－（2x－3y）2