已知二次函数 (a、m为常数,且a¹0)。
(a、m为常数,且a¹0)。
(1)求证:不论a与m为何值,该函数的图像与x轴总有两个公共点;
(2)设该函数的图像的顶点为C,与x轴交于A、B两点,与y轴交于点D。
①当△ABC的面积等于1时,求a的值:
②当△ABC的面积与△ABD的面积相等时,求m的值。
某公园有一个抛物线形状的观景拱桥ABC,其横截面如图所示,在图中建立的直角坐标系中,抛物线的解析式为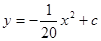 且过顶点C(0,5)(长度单位:m)
且过顶点C(0,5)(长度单位:m)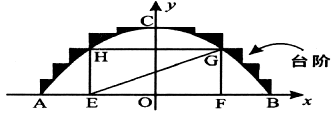
(1)直接写出c的值;
(2)现因搞庆典活动,计划沿拱桥的台阶表面铺设一条宽度为1.5 m的地毯,地毯的价格为20元/m2,求购买地毯需多少元?
(3)在拱桥加固维修时,搭建的“脚手架”为矩形EFGH(H、G分别在抛物线的左右侧上),并铺设斜面EG.已知矩形EFGH的周长为27.5m,求点G的坐标.
如图,在△ABC中,∠ABC=90°,D是边AC上的一点,连接BD,使∠A=2∠1,E是BC上的一点,以BE为直径的圆O经过点D
(1)求证:AC是⊙O的切线;
(2)若∠A=60°,⊙O的半径为2,求阴影部分的面积(结果保留根号和π).
如图,在Rt△ABC中,∠ACB=90°,过C直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.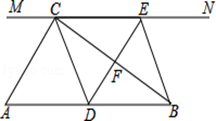
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.
如图:一次函数的图象与反比例函数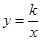 的图象交于A(-2,6)和点B(4,n)
的图象交于A(-2,6)和点B(4,n)
(1)求反比例函数的解析式和B点坐标
(2)根据图象直接回答,在什么范围时,一次函数的值大于反比例函数的值.
如图,一农户要建一个矩形猪舍,猪舍的一边利用长为12m的住房墙,另外三边用25m长的建筑材料围成,为方便进出,在垂直于住房墙的一边留一个1m宽的门,所围矩形猪舍的长、宽分别为多少时,猪舍面积为80m2?