已知圆C经过P(4,-2),Q(-1,3)两点,且在y轴上截得的线段长为4 ,半径小于5.
,半径小于5.
(Ⅰ)求直线PQ与圆C的方程;
(Ⅱ)若直线l∥PQ,直线l与圆C交于点A,B且以线段AB为直径的圆经过坐标原点,求直线l的方程.
已知椭圆E的长轴的一个端点是抛物线 的焦点,离心率是
的焦点,离心率是
(1)求椭圆E的方程;
(2)过点C(—1,0),斜率为k的动直线与椭圆E相交于A、B两点,请问x轴上是否存在点M,使 为常数?若存在,求出点M的坐标;若不存在,请说明理由。
为常数?若存在,求出点M的坐标;若不存在,请说明理由。
某班同学利用寒假在三个小区进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,这两族人数占各自小区总人数的比例如下:
(1)从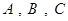 三个社区中各选一人,求恰好有2人是低碳族的概率;
三个社区中各选一人,求恰好有2人是低碳族的概率;
(2)在B小区中随机选择20户,从中抽取的3户中“非低碳族”数量为X,求X的分布列和期望EX.
如图,在四棱柱 中,侧面
中,侧面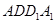 ⊥底面
⊥底面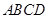 ,
, ,底面
,底面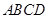 为直角梯形,其中
为直角梯形,其中
 ,O为
,O为 中点。
中点。
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求锐二面角A—C1D1—C的余弦值。
设数列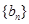 的前
的前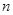 项和为
项和为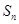 ,且
,且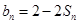 ;数列
;数列 为等差数列,且
为等差数列,且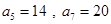 .
.
(1)求数列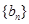 的通项公式;
的通项公式;
(2)若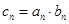 (
(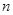 =1,2,3…),
=1,2,3…), 为数列
为数列 的前
的前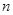 项和.求
项和.求 .
.
已知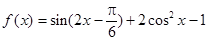
(Ⅰ)求函数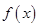 的单调增区间
的单调增区间
(Ⅱ)在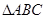 中,
中,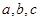 分别是角
分别是角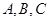 的对边,且
的对边,且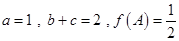 ,求
,求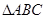 的面积
的面积