(本小题满分15分)已知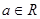 ,函数
,函数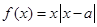 ,
,
(Ⅰ)当 =2时,写出函数
=2时,写出函数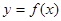 的单调递增区间;
的单调递增区间;
(Ⅱ)当 >2时,求函数
>2时,求函数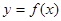 在区间
在区间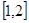 上的最小值;
上的最小值;
(Ⅲ)设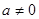 ,函数
,函数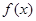 在
在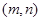 上既有最大值又有最小值,请分别求出
上既有最大值又有最小值,请分别求出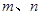 的取值范围(用
的取值范围(用 表示)
表示)
已知直线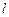 过椭圆E:
过椭圆E: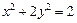 的右焦点
的右焦点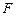 ,且与E相交于
,且与E相交于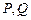 两点.
两点.
(1)设 (
( 为原点),求点
为原点),求点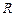 的轨迹方程;
的轨迹方程;
(2)若直线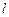 的倾斜角为
的倾斜角为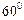 ,求
,求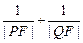 的值.
的值.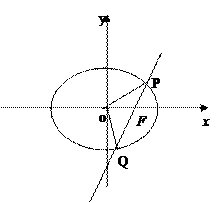
已知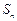 是数列
是数列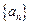 的前
的前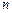 项和,
项和, ,且
,且 ,其中
,其中 .
.
(1)求数列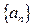 的通项公式
的通项公式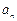 ;
;
(2)计算 的值.
的值.
设函数 ,已知关于
,已知关于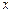 的方程
的方程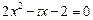 的两个根为
的两个根为 ,
,
(1)判断 在
在 上的单调性;
上的单调性;
(2)若 ,证明
,证明 .
.
在直三棱柱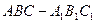 中,
中, ∠ACB=90°,M是
∠ACB=90°,M是 的中点,N是
的中点,N是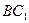 的中点。
的中点。
(1)求证:MN∥平面 ;
;
(2)求点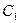 到平面BMC的距离;
到平面BMC的距离;
(3)求二面角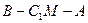 1的大小。
1的大小。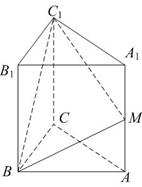
(本题12分)在一次国际比赛中,中国女排与俄罗斯女排以“五局三胜”制进行决赛,根据以往战况,中国女排在每一局中赢的概率都是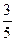 ,已知比赛中,俄罗斯女排先赢了第一局,求:
,已知比赛中,俄罗斯女排先赢了第一局,求:
(1)中国女排在这种情况下取胜的概率;
(2)设比赛局数为 ,求
,求 的分布列及
的分布列及 (均用分数作答).
(均用分数作答).