随着我国汽车产业的发展,城市道路拥堵问题日益严峻.某部门对15个城市的交通状况进行了调查,得到的数据如下表所示:
| 项目 |
北京 |
太原 |
杭州 |
沈阳 |
广州 |
深圳 |
上海 |
桂林 |
南通 |
海口 |
南京 |
温州 |
威海 |
兰州 |
中山 |
| 上班花费时间(分钟) |
52 |
33 |
34 |
34 |
48 |
46 |
47 |
23 |
24 |
24 |
37 |
25 |
24 |
25 |
18 |
| 上班堵车时间(分钟) |
14 |
12 |
12 |
12 |
12 |
11 |
11 |
7 |
7 |
6 |
6 |
5 |
5 |
5 |
0 |
(1)根据上班花费时间,将下面的频数分布直方图补充完整;
(2)求15个城市的平均上班堵车时间(计算结果保留一位小数);
(3)规定: ,比如:
,比如: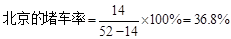 ;
;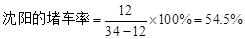 .某人欲从北京、沈阳、上海、温州四个城市中任意选取两个作为出发目的地,求选取的两个城市的堵车率都超过30%的概率.
.某人欲从北京、沈阳、上海、温州四个城市中任意选取两个作为出发目的地,求选取的两个城市的堵车率都超过30%的概率.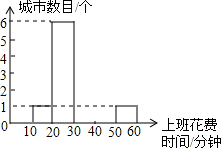
能够完全重合的平行四边形纸片 和 按图①方式摆放,其中 , .点 , 分别在边 , 上, 与 相交于点 .
【探究】求证:四边形 是菱形.
【操作一】固定图①中的平行四边形纸片 ,将平行四边形纸片 绕着点 顺时针旋转一定的角度,使点 与点 重合,如图②.则这两张平行四边形纸片未重叠部分图形的周长和为 .
【操作二】将图②中的平行四边形纸片 绕着点 继续顺时针旋转一定的角度,使点 与点 重合,连接 , ,如图③,若 ,则四边形 的面积为 .

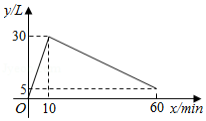
某种机器工作前先将空油箱加满,然后停止加油立即开始工作.当停止工作时,油箱中油量为 ,在整个过程中,油箱里的油量 (单位: 与时间 (单位: 之间的关系如图所示.
(1)机器每分钟加油量为 ,机器工作的过程中每分钟耗油量为 .
(2)求机器工作时 关于 的函数解析式,并写出自变量 的取值范围.
(3)直接写出油箱中油量为油箱容积的一半时 的值.
2020年3月线上授课期间,小莹、小静和小新为了解所在学校九年级600名学生居家减压方式情况,对该校九年级部分学生居家减压方式进行抽样调查.将居家减压方式分为 (享受美食)、 (交流谈心)、 (室内体育活动)、 (听音乐)和 (其他方式)五类,要求每位被调查者选择一种自己最常用的减压方式.他们将收集的数据进行了整理,绘制的统计表分别为表1、表2和表3.
表1:小莹抽取60名男生居家减压方式统计表(单位:人)
|
减压方式 |
|
|
|
|
|
|
人数 |
4 |
6 |
37 |
8 |
5 |
表2:小静随机抽取10名学生居家减压方式统计表(单位:人)
|
减压方式 |
|
|
|
|
|
|
人数 |
2 |
1 |
3 |
3 |
1 |
表3:小新随机抽取60名学生居家减压方式统计表(单位:人)
|
减压方式 |
|
|
|
|
|
|
人数 |
6 |
5 |
26 |
13 |
10 |
根据以上材料,回答下列问题:
(1)小莹、小静和小新三人中,哪一位同学抽样调查的数据能较好地反映出该校九年级学生居家减压方式情况,并简要说明其他两位同学抽样调查的不足之处.
(2)根据三人中能较好地反映出该校九年级居家减压方式的调查结果,估计该校九年级600名学生中利用室内体育活动方式进行减压的人数.
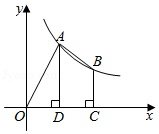
如图,在平面直角坐标系中, 为坐标原点,点 , 在函数 的图象上(点 的横坐标大于点 的横坐标),点 的坐标为 ,过点 作 轴于点 ,过点 作 轴于点 ,连接 , .
(1)求 的值.
(2)若 为 中点,求四边形 的面积.
如图,某班数学小组测量塔的高度,在与塔底部 相距 的 处,用高 的测角仪 测得该塔顶端 的仰角 为 .求塔 的高度(结果精确到 .
(参考数据: , ,
