为了改善市民的生活环境，我是在某河滨空地处修建一个如图所示的休闲文化广场.在Rt△ABC内修建矩形水池DEFG，使顶点D、E在斜边AB上，F、G分别在直角边BC、AC上；又分别以AB、BC、AC为直径作半圆，它们交出两弯新月（图中阴影部分），两弯新月部分栽植花草；其余空地铺设地砖.其中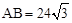
米，∠BAC=600.设EF=x米，DE=y米.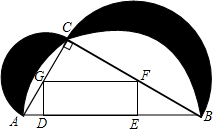
（1）求y与x之间的函数解析式；
（2）当x为何值时，矩形DEFG的面积最大？最大面积是多少？
（3）求两弯新月（图中阴影部分）的面积，并求当x为何值时，矩形DEFG的面积等于两弯新月面积的
？
列方程解应用题：
暑假，某校七年级（1）班组织学生去公园游玩，该班有50名同学组织了划船活动，如图是划船须知. 他们一共租了10条船，并且每条船都坐满了人，
（1）大、小船各租了几条？(6分)
（2）他们租船一共花了多少元钱？(2分)
如图，直线
与
相交于点
， 
平分
。
（1）写出
与
之间的数量关系：；(2分)
（2）若
，求
的度数。(6分)
先化简，再求值：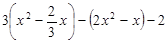
，其中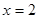
．
解方程：（每小题4分，共8分）
（1）
（2）
某市电话拨号上网有两种收费方式，用户可以任选其一：
A．计时制：0.05元每分钟；
B．包月制：60元每月（限一部个人住宅电话上网）；
此外，每一种上网方式都得加收通信费0.02元每分钟．
（1）某用户某月上网的时间为x小时，请分别写出两种收费方式下该用户应该支付的费用；
（2）若某用户估计一个月内上网的时间为25小时，你认为采用哪种方式较为合算？