(1)计算: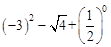 ;(2)解不等式组:
;(2)解不等式组: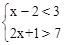 。
。
实践与探究:如图,已知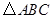 中,
中,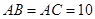 厘米,
厘米,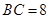 厘米,点
厘米,点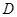 为
为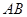 的中点.如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
的中点.如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.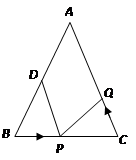
(1)用含有t的代数式表示CP
(2)若点Q的运动速度与点P的运动速度相等,经过1秒后,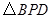 与
与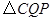 是否全等,请说明理由;
是否全等,请说明理由;
(3)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使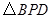 与
与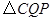 全等?
全等?
某公司每月付给销售人员的工资有两种方案.
方案一:没有底薪,只拿销售提成;方案二:底薪加销售提成(注:销售提成是指从销售每件商品得到的销售额中提取一定数量的费用).
设销售商品的数量 (件),销售人员的月工资
(件),销售人员的月工资 (元).如图所示,
(元).如图所示, 为方案一的函数图象,
为方案一的函数图象, 为方案二的函数图象.从图中信息解答如下问题:
为方案二的函数图象.从图中信息解答如下问题:
(1)求 、
、 与x的函数关系式;
与x的函数关系式;
(2)请问方案二中每月付给销售人员的底薪是多少元?
(3)如果该公司销售人员小丽当月的月工资要为1800元,那么你认为小丽选用哪种方案销售件数少些?销售件数为多少?
为了普及环保知识,增强环保意识,某中学组织了环保知识竞赛活动,初中三个年级根据初赛成绩分别选出了10名同学参加决赛,这些选手的决赛成绩(满分为100分)如下表所示:
| 决赛成绩(单位:分) |
|
| 初一年级 |
80 86 88 80 88 99 80 74 91 89 |
| 初二年级 |
85 85 87 97 85 76 88 77 87 88 |
| 初三年级 |
82 80 78 78 81 96 97 88 89 86 |
(1)请你填写下表:
| 平均分 |
众数 |
中位数 |
|
| 初一年级 |
85.5 |
87 |
|
| 初二年级 |
85.5 |
85 |
|
| 初三年级 |
84 |
(2)请从以下两个不同的角度对三个年级的决赛成绩进行分析:
①从众数和平均数相结合看(分析哪个年级成绩好些);
②从平均数和中位数相结合看(分析哪个年级成绩好些)。
(3)如果在每个年级参加决赛的选手中分别选出3人参加总决赛,你认为哪个年级的实力更强些?并说明理由。
如图,若在象棋盘上建立直角坐标系,使“帥”位于点(-2,-3),“馬”位于点(1,-3),
(1)画出所建立的平面直角坐标系;
(2)分别写出“兵”和“炮”两点位于你所建立的平面直角坐标系的坐标。