抛物线
与x轴交于A，B两点（点A在点B左侧），与y轴交于点C，点D为顶点．
（1）求点B及点D的坐标．
（2）连结BD，CD，抛物线的对称轴与x轴交于点E．
①若线段BD上一点P，使∠DCP=∠BDE，求点P的坐标．
②若抛物线上一点M，作MN⊥CD，交直线CD于点N，使∠CMN=∠BDE，求点M的坐标．
化简下列各式
⑴ 2(3a－5)+5
⑵ －2x－(3x－1)
如图，抛物线y=
x2+bx－2与x轴交于A、B两点，与y轴交于C点，且A（一1，0）．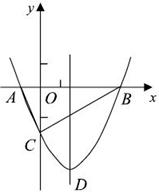
(1)求抛物线的解析式及顶点D的坐标；
(2)判断△ABC的形状，证明你的结论；
(3)点M(m，0)是x轴上的一个动点，当CM+DM的值最小时，求m的值．
已知：□ABCD的两边AB，AD的长是关于x的方程
的两个实数根.
（1）当m为何值时，四边形ABCD是菱形？求出这时菱形的边长；
（2）若AB的长为2，那么□ABCD的周长是多少？
某中学为落实市教育局提出的“全员育人，创办特色学校”的会议精神，决心打造“书香校园”，计划用不超过1900本科技类书籍和1620本人文类书籍，组建中、小型两类图书角共30个.已知组建一个中型图书角需科技类书籍80本，人文类书籍50本；组建一个小型图书角需科技类书籍30本，人文类书籍60本．
（1）符合题意的组建方案有几种？请你帮学校设计出来；
（2）若组建一个中型图书角的费用是860元，组建一个小型图书角的费用是570元，试说明（1）中哪种方案费用最低，最低费用是多少元？
如图，BD为⊙O的直径，AB=AC，AD交BC于点E，AE=2，ED=4，
(1)求证：△ABE∽△ADB；
(2)求AB的长；
(3)延长DB到F，使得BF=BO，连接FA，试判断直线FA与⊙O的位置关系，并说明理由．