极坐标系与直角坐标系xOy有相同的长度单位,以原点D为极点,以x轴正半轴为极轴,曲线Cl的极坐标方程为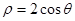 ,曲线C2的参数方程为
,曲线C2的参数方程为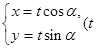 为参数)。
为参数)。
(1)当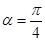 时,求曲线Cl与C2公共点的直角坐标;
时,求曲线Cl与C2公共点的直角坐标;
(2)若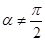 ,当
,当 变化时,设曲线C1与C2的公共点为A,B,试求AB中点M轨迹的极坐标方程,并指出它表示什么曲线.
变化时,设曲线C1与C2的公共点为A,B,试求AB中点M轨迹的极坐标方程,并指出它表示什么曲线.
经调查发现,人们长期食用含高浓度甲基汞的鱼类会引起汞中毒,其中罗非鱼体内汞含量比其它鱼偏高.现从一批数量很大的罗非鱼中随机地抽出 条作样本,经检测得各条鱼的汞含量的茎叶图(以小数点前的数字为茎,小数点后一位数字为叶)如下:
条作样本,经检测得各条鱼的汞含量的茎叶图(以小数点前的数字为茎,小数点后一位数字为叶)如下:
罗非鱼的汞含量(ppm)
 |
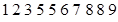 |
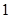 |
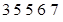 |
《中华人民共和国环境保护法》规定食品的汞含量不得超过 ppm.
ppm.
(1)检查人员从这 条鱼中,随机抽出
条鱼中,随机抽出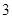 条,求
条,求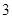 条中恰有
条中恰有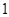 条汞含量超标的概率;
条汞含量超标的概率;
(2)若从这批数量很大的鱼中任选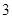 条鱼,记
条鱼,记 表示抽到的汞含量超标的鱼的条数.以此
表示抽到的汞含量超标的鱼的条数.以此 条鱼的样本数据来估计这批数量很大的鱼的总体数据,求
条鱼的样本数据来估计这批数量很大的鱼的总体数据,求 的分布列及数学期望
的分布列及数学期望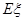 .
.
在△ 中,角
中,角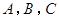 的对边分别为
的对边分别为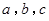 ,且
,且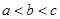 ,
, .
.
(1)求角 的大小;
的大小;
(2)若 ,
, ,求
,求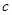 边的长和△
边的长和△ 的面积.
的面积.
设进入某商场的每一位顾客购买甲种商品的概率为0.5,购买乙种商品的概率为0.6,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品是相互独立的.
(1)求进入该商场的1位顾客购买甲、乙两种商品中的一种的概率;
(2)求进入该商场的3位顾客中,至少有2位顾客既未购买甲种商品也未购买乙种商品的概率.
某计算机程序每运行一次都随机出现一个五位的二进制数A=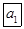
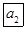


 ,其中A的各位数中,a1=1,ak(k=2,3,4,5)出现0的概率为
,其中A的各位数中,a1=1,ak(k=2,3,4,5)出现0的概率为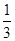 ,出现1的概率为
,出现1的概率为 .记X=a1+a2+a3+a4+a5,当程序运行一次时,
.记X=a1+a2+a3+a4+a5,当程序运行一次时,
(1)求X=3的概率;
(2)求X的分布列.
某大厦的一部电梯从底层出发后只能在第18,19,20层可以停靠,若该电梯在底层载有5位乘客,且每位乘客在这三层的每一层下电梯的概率均为 ,用X表示这5位乘客在第20层下电梯的人数,求随机变量X的分布列.
,用X表示这5位乘客在第20层下电梯的人数,求随机变量X的分布列.