经调查发现,人们长期食用含高浓度甲基汞的鱼类会引起汞中毒,其中罗非鱼体内汞含量比其它鱼偏高.现从一批数量很大的罗非鱼中随机地抽出 条作样本,经检测得各条鱼的汞含量的茎叶图(以小数点前的数字为茎,小数点后一位数字为叶)如下:
条作样本,经检测得各条鱼的汞含量的茎叶图(以小数点前的数字为茎,小数点后一位数字为叶)如下:
罗非鱼的汞含量(ppm)
 |
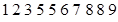 |
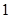 |
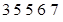 |
《中华人民共和国环境保护法》规定食品的汞含量不得超过 ppm.
ppm.
(1)检查人员从这 条鱼中,随机抽出
条鱼中,随机抽出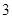 条,求
条,求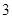 条中恰有
条中恰有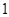 条汞含量超标的概率;
条汞含量超标的概率;
(2)若从这批数量很大的鱼中任选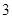 条鱼,记
条鱼,记 表示抽到的汞含量超标的鱼的条数.以此
表示抽到的汞含量超标的鱼的条数.以此 条鱼的样本数据来估计这批数量很大的鱼的总体数据,求
条鱼的样本数据来估计这批数量很大的鱼的总体数据,求 的分布列及数学期望
的分布列及数学期望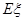 .
.