已知某池塘养殖着鲤鱼和鲫鱼,为了估计这两种鱼的数量,养殖者从池塘中捕出两种鱼各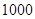 只,给每只鱼做上不影响其存活的标记,然后放回池塘,待完全混合后,再每次从池塘中随机的捕出
只,给每只鱼做上不影响其存活的标记,然后放回池塘,待完全混合后,再每次从池塘中随机的捕出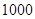 只鱼,记录下其中有记号的鱼的数目,立即放回池塘中。这样的记录做了
只鱼,记录下其中有记号的鱼的数目,立即放回池塘中。这样的记录做了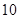 次,并将记录获取的数据做成以下的茎叶图。
次,并将记录获取的数据做成以下的茎叶图。
(Ⅰ)根据茎叶图计算有记号的鲤鱼和鲫鱼数目的平均数,并估计池塘中的鲤鱼和鲫鱼的数量;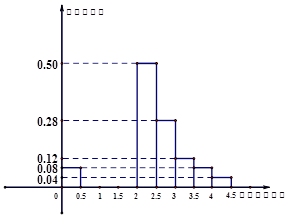
(Ⅱ)为了估计池塘中鱼的总重量,现从中按照(Ⅰ)的比例对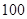 条鱼进行称重,据称重鱼的重量介于
条鱼进行称重,据称重鱼的重量介于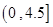 (单位:千克)之间,将测量结果按如下方式分成九组:第一组
(单位:千克)之间,将测量结果按如下方式分成九组:第一组 、第二组
、第二组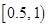 ;……,第九组
;……,第九组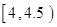 。右图是按上述分组方法得到的频率分布直方图的一部分。
。右图是按上述分组方法得到的频率分布直方图的一部分。
①估计池塘中鱼的重量在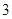 千克以上(含
千克以上(含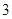 千克)的条数;
千克)的条数;
②若第二组、第三组、第四组鱼的条数依次成公差为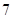 的等差数列,请将频率分布直方图补充完整;
的等差数列,请将频率分布直方图补充完整;
③在②的条件下估计池塘中鱼的重量的众数、中位数及估计池塘中鱼的总重量;
(Ⅲ)假设随机地从池塘逐只有放回的捕出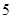 只鱼中出现鲤鱼的次数为
只鱼中出现鲤鱼的次数为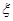 ,求
,求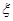 的数学期望。
的数学期望。

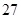
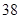
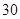
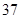
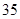
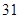

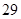
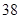
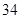
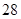
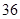 为了选拔参加奥运会选手,教练员对甲,乙自行车运动员进行测试,测得他们的最大速度
为了选拔参加奥运会选手,教练员对甲,乙自行车运动员进行测试,测得他们的最大速度
的数据如下表所示(单位m/s)
请判断谁参加这项重大比赛更合适,并阐述理由。
. (满分12分) 某班同学利用国庆节进行社会实践,对[25,55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
| 组数 |
分组 |
低碳族的人数 |
占本组的频率 |
| 第一组 |
[25,30) |
120 |
0.6 |
| 第二组 |
[30,35) |
195 |
p |
| 第三组 |
[35,40) |
100 |
0.5 |
| 第四组 |
[40,45) |
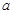 |
0.4 |
| 第五组 |
[45,50) |
30 |
0.3 |
| 第六组 |
[50,55) |
15 |
0.3 |
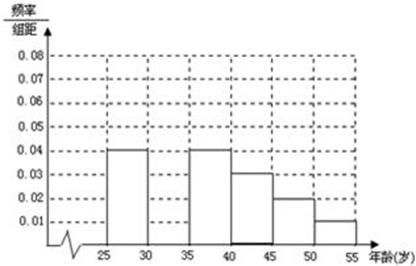
(Ⅰ)补全频率分布直方图,并求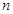 、
、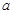 、
、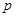 的值;
的值;
(Ⅱ)从年龄段在[40,50)的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中恰有1人年龄在[40,45)岁的概率.
(本小题满分12分)
经统计,某大型商场一个结算窗口每天排队结算的人数及相应的概率如下:
| 排队人数 |
0~5 |
6~10 |
11~15 |
16~20 |
21~25 |
25人以上 |
| 概率 |
0.1 |
0.15 |
0.25 |
0.25 |
0.2 |
0.05 |
(1)求每天不超过20人排队结算的概率;
(2)一周7天中,若有3天以上(含3天)出现超过15人排队结算的概率大于0.75,商场就需要增加结算窗口,试问该商场是否需要产加结算窗口?
从4名男生和5名女 生中任选5人参加数学课外小组,求在下列条件下各有多少种不同的选法?
生中任选5人参加数学课外小组,求在下列条件下各有多少种不同的选法?
(1) 选2名男生和3名女生,且女生甲必须入选;
选2名男生和3名女生,且女生甲必须入选;
(2)至多选4名女生,且男生甲和女生乙不同时入选.
.(满分10分)由经验得知,在某商场付款处排队等候付款的人数及概率如下表:
| 排队人数 |
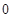 |
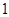 |
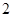 |
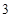 |
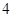 |
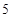 人以上 人以上 |
| 概率 |
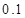 |
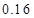 |
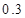 |
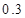 |
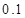 |
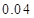 |
(I)至多有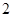 人排队的概率是多少?
人排队的概率是多少?
(II)至少有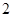 人排队的概率是多少
人排队的概率是多少