已知=(sinθ,),=(1,),其中θ∈(π,),则一定有( )
| A.∥ | B.⊥ | C.与夹角为45° | D.||=|| |
已知抛物线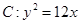 ,点
,点 ,过
,过 的直线
的直线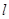 交抛物线
交抛物线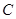 于
于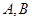 两点.
两点.
(1)若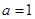 ,抛物线
,抛物线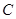 的焦点与
的焦点与 中点的连线垂直于
中点的连线垂直于 轴,求直线
轴,求直线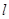 的方程;
的方程;
(2)设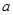 为小于零的常数,点
为小于零的常数,点 关于
关于 轴的对称点为
轴的对称点为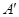 ,求证:直线
,求证:直线 过定点
过定点
如图,四棱锥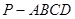 中,底面
中,底面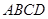 为梯形,
为梯形,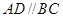 ,
,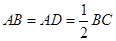 ,
,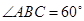 ,平面
,平面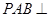 平面
平面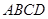 ,
,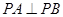 .
.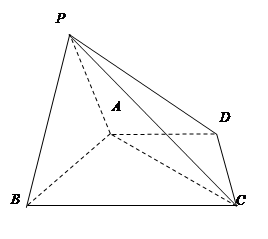
(1)求证: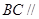 平面
平面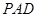 ;
;
(2)求证: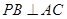 ;
;
(3)是否存在点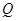 ,到四棱锥
,到四棱锥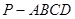 各顶点的距离都相等?并说明理由.
各顶点的距离都相等?并说明理由.
已知椭圆 的离心率为
的离心率为 ,左右焦点分别为
,左右焦点分别为 ,且
,且 .
.
(1)求椭圆C的方程;
(2)过点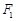 的直线与椭圆
的直线与椭圆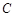 相交于
相交于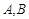 两点,且
两点,且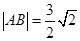 ,求
,求 的面积.
的面积.
在斜三棱柱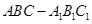 中,侧面
中,侧面 平面
平面 ,
, ,
,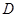 为
为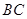 中点.
中点.
(1)求证: ;
;
(2)求证: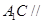 平面
平面 ;
;
(3)若 ,
,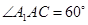 ,求三棱锥
,求三棱锥 的体积.
的体积.
已知圆 经过坐标原点
经过坐标原点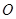 和点
和点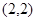 ,且圆心在
,且圆心在 轴上.
轴上.
(1)求圆 的方程;
的方程;
(2)设直线 经过点
经过点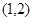 ,且
,且 与圆
与圆 相交所得弦长为
相交所得弦长为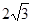 ,求直线
,求直线 的方程.
的方程.