有依次排列的3个数:3,9,8,对任相邻的两个数,都用右边的数减去左边的数,所得之差写在这两个数之间,可产生一个新数串:3,6,9,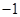 ,8,这称为第一次操作;做第二次同样的操作后也可产生一个新数串:3,3,6,3,9,
,8,这称为第一次操作;做第二次同样的操作后也可产生一个新数串:3,3,6,3,9,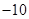 ,
,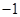 ,9,8,继续依次操作下去,问:从数串3,9,8开始操作第一百次以后所产生的那个新数串的所有数之和是多少?
,9,8,继续依次操作下去,问:从数串3,9,8开始操作第一百次以后所产生的那个新数串的所有数之和是多少?
如图,已知∠AOB,OA=OB,点E在OB上,且四边形AEBF是平行四边形.请你只用无刻度的直尺在图中画出∠AOB的平分线(保留画图痕迹,不写画法),并说明理由.
先化简,再求值。
解方程:(1)2( -3)(
-3)( +1)=
+1)= +1.
+1.
计算:(1)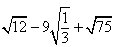
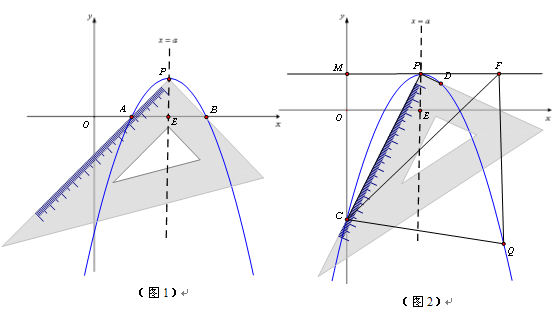
把一块三角板置于平面直角坐标系中,三角板的直角顶点为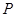 ,两直角边与
,两直角边与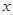 轴交于
轴交于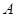 、
、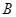 ,如图1,测得
,如图1,测得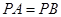 ,
, .以
.以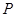 为顶点的抛物线
为顶点的抛物线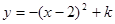 恰好经过
恰好经过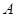 、
、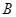 两点,抛物线的对称轴
两点,抛物线的对称轴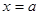 与
与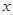 轴交于点
轴交于点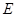 .
.
(1) 填空: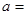 ,
,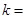 ,点
,点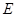 的坐标为;
的坐标为;
(2)设抛物线与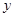 轴交于点
轴交于点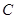 ,过
,过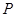 作直线
作直线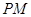 ⊥
⊥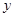 轴,垂足为
轴,垂足为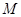 .如图2,把三角板绕着点
.如图2,把三角板绕着点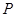 旋转一定角度,使其中一条直角边恰好过点
旋转一定角度,使其中一条直角边恰好过点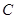 ,另一条直角边与抛物线的交点为
,另一条直角边与抛物线的交点为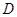 ,试问:点
,试问:点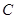 、
、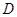 、
、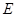 三点是否在同一直线上?请说明理由.
三点是否在同一直线上?请说明理由.
(3)在(2)的条件下,若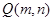 为抛物线上的一动点, 连结
为抛物线上的一动点, 连结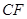 、
、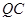 ,过
,过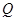 作
作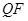 ⊥
⊥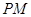 ,垂足为
,垂足为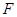 .试探索:是否存在点
.试探索:是否存在点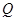 ,使得
,使得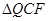 是以
是以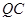 为腰的等腰三角形?若存在,请求出
为腰的等腰三角形?若存在,请求出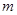 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.