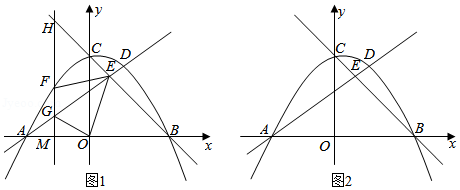
把一块三角板置于平面直角坐标系中,三角板的直角顶点为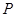 ,两直角边与
,两直角边与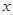 轴交于
轴交于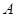 、
、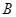 ,如图1,测得
,如图1,测得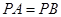 ,
, .以
.以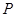 为顶点的抛物线
为顶点的抛物线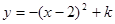 恰好经过
恰好经过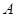 、
、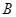 两点,抛物线的对称轴
两点,抛物线的对称轴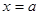 与
与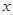 轴交于点
轴交于点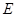 .
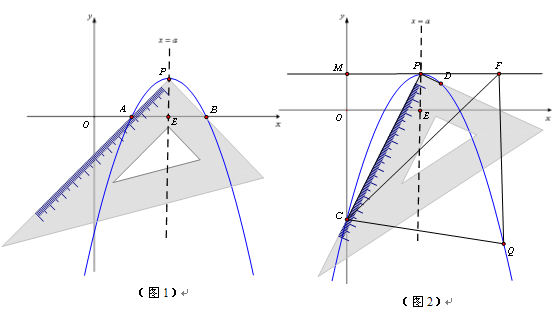
.
(1) 填空: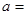 ,
,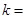 ,点
,点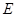 的坐标为 ;
的坐标为 ;
(2)设抛物线与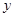 轴交于点
轴交于点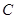 ,过
,过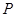 作直线
作直线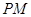 ⊥
⊥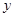 轴,垂足为
轴,垂足为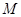 .如图2,把三角板绕着点
.如图2,把三角板绕着点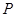 旋转一定角度,使其中一条直角边恰好过点
旋转一定角度,使其中一条直角边恰好过点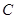 ,另一条直角边与抛物线的交点为
,另一条直角边与抛物线的交点为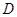 ,试问:点
,试问:点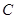 、
、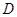 、
、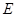 三点是否在同一直线上?请说明理由.
三点是否在同一直线上?请说明理由.
(3)在(2)的条件下,若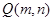 为抛物线上的一动点, 连结
为抛物线上的一动点, 连结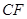 、
、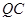 ,过
,过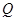 作
作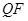 ⊥
⊥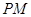 ,垂足为
,垂足为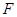 .试探索:是否存在点
.试探索:是否存在点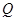 ,使得
,使得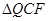 是以
是以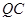 为腰的等腰三角形?若存在,请求出
为腰的等腰三角形?若存在,请求出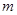 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
如图, 、 两点的坐标分别为 , ,将线段 绕点 逆时针旋转 得到线段 ,过点 作 ,垂足为 ,反比例函数 的图象经过点 .
(1)直接写出点 的坐标,并求反比例函数的解析式;
(2)点 在反比例函数 的图象上,当 的面积为3时,求点 的坐标.
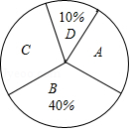
某校为了解学生课外阅读时间情况,随机抽取了 名学生,根据平均每天课外阅读时间的长短,将他们分为 , , , 四个组别,并绘制了如图不完整的频数分布表和扇形统计图.
频数分布表
|
组别 |
时间 (小时) |
频 人数 |
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
5 |
请根据图表中的信息解答下列问题:
(1)求 与 的值,并补全扇形统计图;
(2)直接写出所抽取的 名学生平均每天课外阅读时间的中位数落在的组别;
(3)该校现有1500名学生,请你估计该校有多少名学生平均每天课外阅读时间不少于1小时.
有四张正面分别标有数字1,2,3,4的不透明卡片,它们除数字外无其他差别,现将它们背面朝上洗匀.
(1)随机抽取一张卡片,卡片上的数字是奇数的概率为 .
(2)随机抽取一张卡片,然后放回洗匀,再随机抽取一张卡片,请用列表或画树状图的方法,求两次抽取的卡片上的数字和等于6的概率.
先化简,再求值: ,其中 .
在平面直角坐标系中,抛物线 交 轴于 , 两点,交 轴于点 .
(1)求抛物线的表达式;
(2)如图,直线 与抛物线交于 , 两点,与直线 交于点 .若 是线段 上的动点,过点 作 轴的垂线,交抛物线于点 ,交直线 于点 ,交直线 于点 .
①当点 在直线 上方的抛物线上,且 时,求 的值;
②在平面内是否在点 ,使四边形 为正方形?若存在,请直接写出点 的坐标;若不存在,请说明理由.