若a,b,cÎR+,且a+b+c=1,求 的最大值.
的最大值.
(13分)如图,在边长为2的菱形 中,
中,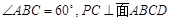 ,
,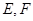 是
是 和
和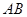 的中点.(Ⅰ)求证:
的中点.(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)若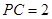 ,求
,求 与平面
与平面 所成角的正弦值.
所成角的正弦值.
(13分)如图,正方体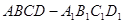 中.
中.
(Ⅰ)求 与
与 所成角的大小;
所成角的大小;
(Ⅱ)求二面角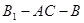 的正切值.
的正切值.
某厂生产某种零件,每个零件的成本为40元,出厂单价60元,该厂为鼓励销售商订购。决定当一次订购超过100个时,每多订购一个,订购的全部零件的出厂单价就降低0.02元,但实际出厂价不低于51元.
(1)当一次订购量为多少时,零件的实际出厂单价降为51元?
(2)当一次订购量为x个,零件的实际出厂单价为p元,写出函数p=f(x)的表达式.
(3)当销售商一次订购500个零件时,该厂获得的利润是多少元?如果订购1000个,利润又是多少?
商店出售茶壶和茶杯,茶壶定价每个20元,茶杯每个5元,该商店推出两种优惠办法:(1)买一个茶壶赠一个茶杯;(2)按总价的92%付款.
某顾客需购买茶壶4个,茶杯若干个(不少于4个),若购买茶杯数x个,付款y(元),分别建立两种优惠办法中y与x之间的函数关系式,并讨论该顾客买同样多的茶杯时,两种办法哪一种更优惠。
设不等式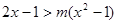 对满足
对满足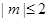 的一切实数
的一切实数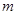 的取值都成立,求
的取值都成立,求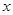 的取值范围。
的取值范围。