某厂生产某种零件,每个零件的成本为40元,出厂单价60元,该厂为鼓励销售商订购。决定当一次订购超过100个时,每多订购一个,订购的全部零件的出厂单价就降低0.02元,但实际出厂价不低于51元.
(1)当一次订购量为多少时,零件的实际出厂单价降为51元?
(2)当一次订购量为x个,零件的实际出厂单价为p元,写出函数p=f(x)的表达式.
(3)当销售商一次订购500个零件时,该厂获得的利润是多少元?如果订购1000个,利润又是多少?
已知函数
的导函数的图象关于直线
对称.
(Ⅰ)求
的值;
(Ⅱ)若
在
处取得最小值,记此极小值为
,求
的定义域和值域.
如图,在正三棱柱 中, , ,点 是 的中点,点 在 上,且 .
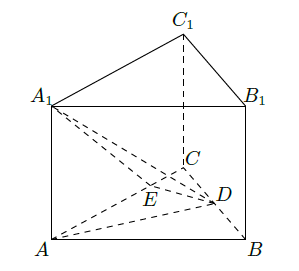
(Ⅰ)证明:平面
(Ⅱ)求直线AD和平面 所成角的正弦值。
已知函数
(其中
)的周期为
,且图象上一个最低点为
.
(Ⅰ)求
的解析式;
(Ⅱ)当
,求
的最值.
已知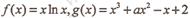
(I)求函数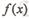 的单调区间;
的单调区间;
(Ⅱ)求函数 上的最小值;
上的最小值;
(Ⅲ)对一切的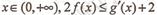 恒成立,求实数a的取值范围
恒成立,求实数a的取值范围
在美化校园的植树活动中,某同学共种了6棵树,各棵树的成活与否是相互独立的, 每棵树成活的概率均为p.已知该同学所种树中有3棵成活的概率为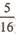 .
.
(I)求p的值;
(II)若有3棵或3棵以上的树未成活,则需要补种,求需要补种的概率;
(Ⅲ)设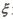 为成活树的棵数,求
为成活树的棵数,求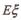 .
.