某高中学校为高一新生设计的学生板凳的正面视图如图所示,其中BA=CD,BC=20cm,BC、EF平行于地面AD且到地面AD的距离分别为40cm、8cm.为使板凳两腿底端A、D之间的距离为50cm,那么横梁EF应为多长?(材质及其厚度等暂忽略不计).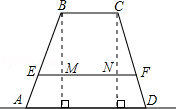
吸烟有害健康,为配合“戒烟”运动,某校组织同学们在社区开展了“你支持哪种戒烟方式”的随机问卷调查,并将调查结果绘制成两幅不完整的统计图: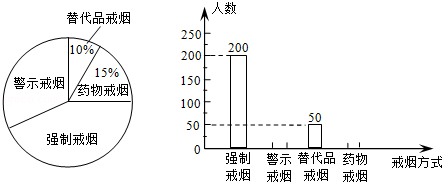
根据统计图解答下列问题:
(1)同学们一共调查了多少人?
(2)将条形统计图补充完整.
(3)若该社区有1万人,请你估计大约有多少人支持“警示戒烟”这种方式?
(4)为了让更多的市民增强“戒烟”意识,同学们在社区做了两期“警示戒烟”的宣传.若每期宣传后,市民支持“警示戒烟”的平均增长率为20%,则两期宣传后支持“警示戒烟”的市民约有多少人?
某学校为了改善办学条件,计划购置一批电子白板和一批笔记本电脑,经投标,购买1块电子白板比买3台笔记本电脑多3000元,购买4块电子白板和5台笔记本电脑共需80000元.
(1)求购买1块电子白板和一台笔记本电脑各需多少元?
(2)根据该校实际情况,需购买电子白板和笔记本电脑的总数为396,要求购买的总费用不超过2700000元,并购买笔记本电脑的台数不超过购买电子白板数量的3倍,该校有哪几种购买方案?
(3)上面的哪种购买方 案最省钱?按最省钱方案购买需要多少钱?
如 图,△ACB和△E CD都是等腰直角三角形,A,C,D三点在同一直线上,连接BD,AE,并延长AE交BD于F.
(1)求证:△ACE≌△BCD;
(2)直线AE与BD互相垂直吗?请证明你的结论.
如图,路灯(P点)距地面8米,身高1.6米的小明从距路灯的底部(O点 )20米的A点,沿OA所在的直线行走14米到B点时,身影的长度是变长了还是变短了?变长或变短了多少米?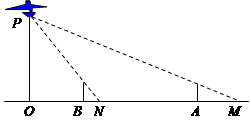
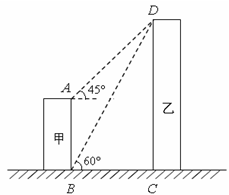
如图,有甲、乙两建筑物,甲建筑物的高度为40 m,AB⊥BC,DC⊥BC,某数学学习小组开展测量乙建筑物高度的实践活动,从B点测得D点的仰角为60°,从A点测得D点的仰角为45°.求乙建筑物的高DC.