如图，在平面直角坐标系中，坐标原点为O，A点坐标为（4，0），B点坐标为（﹣1，0），以AB的中点P为圆心，AB为直径作⊙P的正半轴交于点C．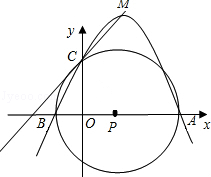
（1）求经过A、B、C三点的抛物线所对应的函数解析式；
（2）设M为（1）中抛物线的顶点，求直线MC对应的函数解析式；
（3）试说明直线MC与⊙P的位置关系，并证明你的结论．
已知，a=
﹣
+1
（1）求a、c的值；
（2）若一元二次方程ax2+bx+c=0有一个根是1，求b的值和方程的另一个根．
已知△ABC在平面直角坐标系中的位置如图所示．
（1）将△ABC绕圆点O旋转180°得到△A1B1C1，请你在图中画出△A1B1C1；
（2）写出点A1的坐标；
（3）求△A1B1C1的面积．
已知，如图点A、B、C在⊙O上，AO∥BC，∠OBC=40°，求∠ACB的度数．
解方程：8x﹣2=x（4﹣x）
如图，在平面直角坐标系中，已知抛物线
交
轴于A（2，0），B（6，0）两点，交
轴于点C（0，
）.
（1）求此抛物线的解析式；
（2）若此抛物线的对称轴与直线
交于点D，作⊙D与x轴相切，⊙D交轴于点E、F两点，求劣弧EF所对圆心角的度数；
（3）P为此抛物线在第二象限图像上的一点，PG垂直于轴，垂足为点G，试确定P点的位置，使得△PGA的面积被直线AC分为1︰2两部分.