为声援扬州“运河申遗”,某校举办了一次运河知识竞赛,满分10分,学生得分为整数,成绩达到6分以上(包括6分)为合格,达到9分以上(包含9分)为优秀.这次竞赛中甲乙两组学生成绩分布的条形统计图如图所示.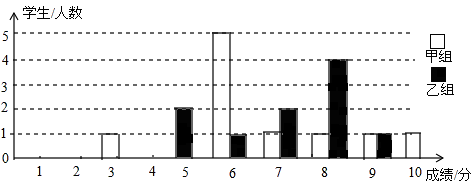
(1)补充完成下面的成绩统计分析表:
| 组别 |
平均分 |
中位数 |
方差 |
合格率 |
优秀率 |
| 甲组 |
6.7 |
|
3.41 |
90% |
20% |
| 乙组 |
|
7.5 |
1.69 |
80% |
10% |
(2)小明同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上表可知,小明是 组的学生;(填“甲”或“乙”)
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你给出两条支持乙组同学观点的理由.
某校为了丰富学生的课外体育活动,购买了排球和跳绳.已知排球的单价是跳绳的单价的3倍,购买跳绳共花费750元,购买排球共花费900元,购买跳绳的数量比购买排球的数量多30个,求跳绳的单价.
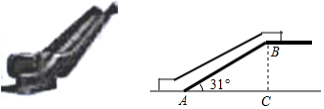
如图,某商店营业大厅自动扶梯 的倾斜角为 , 的长为12米,求大厅两层之间的距离 的长.(结果精确到0.1米)(参考数据: , ,
一个不透明的口袋中有三个小球,上面分别标有字母 , , ,每个小球除字母不同外其余均相同,小园同学从口袋中随机摸出一个小球,记下字母后放回且搅匀,再从可口袋中随机摸出一个小球记下字母.用画树状图(或列表)的方法,求小园同学两次摸出的小球上的字母相同的概率.
如图1,在平面直角坐标系中,点 在 轴正半轴上, 的长度为 ,以 为边向上作等边三角形 ,抛物线 经过点 , , 三点
(1)当 时, ,当 时, ;
(2)根据(1)中的结果,猜想 与 的关系,并证明你的结论;
(3)如图2,在图1的基础上,作 轴的平行线交抛物线 于 、 两点, 的长度为 ,当 为等腰直角三角形时, 和 的关系式为 ;
(4)利用(2)(3)中的结论,求 与 的面积比.

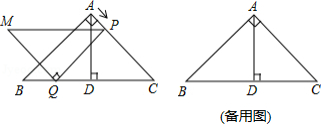
如图,在等腰直角三角形 中, , , 于点 ,点 从点 出发,沿 方向以 的速度运动到点 停止,在运动过程中,过点 作 交 于点 ,以线段 为边作等腰直角三角形 ,且 (点 , 位于 异侧).设点 的运动时间为 , 与 重叠部分的面积为
(1)当点 落在 上时, ;
(2)当点 落在 上时, ;
(3)求 关于 的函数解析式,并写出自变量 的取值范围.