春雷中学要了解全校学生对不同类别电视节目的喜爱情况,围绕“在体育、新闻、动画、娱乐四类电视节目中,你最喜欢哪一类?(必选且只选一类)”的问题,在全校范围内随机抽取部分学生进行问卷调查.将调查结果整理后绘制成如图所示的不完整的条形统计图.其中最喜欢新闻类电视节目的人数占被抽取人数的l0%.请你根据以上信息回答下列问题:
(1)在这次调查中,最喜欢新闻类电视节目的学生有多少名?并补全条形统计图:
(2)如果全校共有l 200名学生,请你估计全校学生中最喜欢体育类电视节目的学生有多少名?
(本题6分)在数轴上把下列各数表示出来,并用“<”连接各数.
2,﹣|﹣1|,1 ,0,﹣(﹣3.5)
,0,﹣(﹣3.5)
如图1,在△ABC中,∠BAC=90°,AB=AC,AE是过A的一条直线,且B,C在AE的异侧,BD⊥AE于点D,CE⊥AE于点E.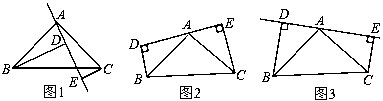
(1)求证:BD=DE+CE;
(2)若直线AE绕点A旋转到图2位置时(BD<CE),其余条件不变,问BD与DE,CE的关系如何,请证明;
(3)若直线AE绕点A旋转到图3时(BD>CE),其余条件不变,BD与DE,CE的关系怎样?请直接写出结果,不须证明.
(4)归纳(1),(2),(3),请用简捷的语言表述BD与DE,CE的关系.
看图回答问题:
(1)内角和为2014°,小明为什么说不可能?
(2)小华求的是几边形的内角和?
(3)错把外角当内角的那个外角的度数你能求出来吗?它是多少度?
如图,O是△ABC内任意一点,连接OB、OC.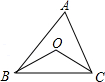
(1)求证:∠BOC>∠A;
(2)比较AB+AC与OB+OC的大小,并说明理由.
如图,已知Rt△ABC≌Rt△ADE,∠ABC=∠ADE=90°,BC与DE相交于点F,连接CD,EB.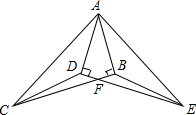
(1)图中还有几对全等三角形,请你一一列举;
(2)求证:CF=EF.