如图，已知二次函数的图象过点A（0，﹣3），B（
），对称轴为直线
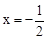，点P是抛物线上的一动点，过点P分别作PM⊥x轴于点M，PN⊥y轴于点N，在四边形PMON上分别截取PC=
MP，MD=OM，OE=ON，NF=NP．
（1）求此二次函数的解析式；
（2）求证：以C、D、E、F为顶点的四边形CDEF是平行四边形；
（3）在抛物线上是否存在这样的点P，使四边形CDEF为矩形？若存在，请求出所有符合条件的P点坐标；若不存在，请说明理由．
AB是⊙O的一条弦，它的中点为M，过点M作一条非直径的弦CD，过点C和D作⊙O的两条切线，分别与直线AB相交于P、Q两点．求证：PA=QB
如图，在四边形ABCD中，AC平分∠BAD，CE⊥AB于点E．
(1)若∠ADC+∠ABC=180°，求证：AD+AB =2AE；
(2)若AD+AB =2AE，求证：CD=CB.
由示意图可见，抛物线y=x2 +px+q①若有两点A（a，yl）、B(b，y2)（其中a<b）在x轴下方，则抛物线必与x轴有两个交点C（x1，O）、D（x2，O）（其中xl<x2），且满足xl<a<b<x2．当A(1，- 2.005)，且xl、x2均为整数时，求二次函数的表达式，
某饮料厂现有A、B两种果汁原料至多分别有19千克和17.2千克，准备配制甲、乙两种新型饮料共50瓶。表中是试验的有关数据：
| 饮料 每瓶新型 饮料含果汁量 |
甲种 新型饮料 |
乙种 新型饮料 |
| A种果汁（单位：千克） |
0.5 |
0.2 |
| B种果汁（单位：千克） |
0.3 |
0.4 |
⑴ 假设甲种饮料需要配制x瓶，请写出满足条件的不等式组
⑵ 通过计算说明有哪几种配制方案
⑶ 设甲种饮料每瓶成本为4元，乙种饮料每瓶成本为3元，这两种饮料的成本总额为y元，通过计算说明，当甲种饮料配制多少瓶时，甲、乙两种饮料的总成本最少？
2008年5月12日14时28分在我国四川省汶川地区发生了里氏8.0级强烈地震,灾情牵动全国人民的心.“一方有难,八方支援”，某厂计划加工1500顶帐篷支援灾区人民,在加工了300顶帐篷后,由于救灾需要,工作效率提高到原来的1.5倍,结果提前4天完成了任务,求原来每天加工多少顶帐篷?