如图，直线x=-4与x轴交于点E，一开口向上的抛物线过原点交线段OE于点A，交直线x=-4于点B，过B且平行于x轴的直线与抛物线交于点C，直线OC交直线AB于D，且AD：BD=1：3．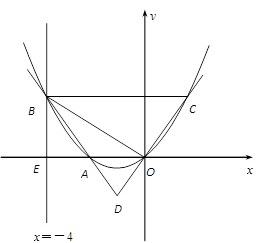
（1）求点A的坐标；
（2）若△OBC是等腰三角形，求此抛物线的函数关系式．
（本小题满分8分）如图，正方形网格中的每个小正方形边长都是1．
（利用网格线进行画图，别忘了标上字母噢！）
（1）在图1中，画一个顶点为格点、面积为5的正方形；
（2）在图2中，已知线段AB、CD，画线段EF，使它与AB、CD组成轴对称图形；
（要求画出所有符合题意的线段）
（3）在图3中，找一格点D，满足：①到CB、CA的距离相等；②到点A、C的距离相等．
（本题满分8分，每小题4分）
（1）计算：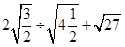
；
（2）求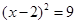
中x的值．
某校对该校七年级（1）班全体学生的血型做了一次全面调查，根据调查结果绘制了下列两幅不完整的统计图，请你根据统计图提供的信息解答以下问题：
（1）该校七年级（1）班有多少名学生．
（2）求出扇形统计图中“O型”血所对扇形的圆心角的度数．
（3）将条形统计图中“B型”血部分的条形图补充完整．
（本题满分8分，其中每问4分）
如图，O为直线AB上一点，∠AOC=50°，OD平分∠AOC，∠DOE=90°．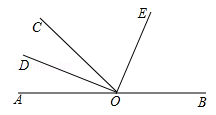
（1）求∠BOD的度数．
（2）请通过计算说明OE平分∠BOC．
（本题满分8分，每小题4分）解方程：
（1）
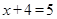
（2）已知方程
是关于x 的一元一次方程．求m的值并解这个一元一次方程．