全国爱眼日是每年的6月6日,2013年世界爱眼日主题确定为“关爱青少年眼健康”,某中学为了解该校学生的视力情况,采用抽样调查的方式,从视力正常、轻度近视、中度近视、重度近视四个方面调查了若干名学生的视力情况,并根据调查结果制作了如下两幅统计图。

根据图中提供的信息解答下列问题:
(1)一共随机调查了多少人?
(2)补全人数统计图;
(3)若该校共有1500名学生,请你估计该校学生视力正常的人数。
设 ,
, ,
, ,…,
,…, 
设 ,则S="_________" (用含n的代数式表示,其中n为正整数).
,则S="_________" (用含n的代数式表示,其中n为正整数).
在三个整式x2-1,x2+2x+1,x2+x中,请你从中任意选择两个,将其中一个作为分子,另一个作为分母组成一个分式,并将这个分式进行化简,再求当x=2时分式的值.
先化简 ,然后从不等组
,然后从不等组 的解集中,选取一个你认为符合题意的x的值代入求值.
的解集中,选取一个你认为符合题意的x的值代入求值.
如图,抛物线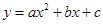 与
与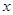 轴交于
轴交于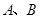 两点,与
两点,与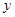 轴相交于点
轴相交于点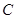 .连结AC、BC,B、C两点的坐标分别为B(1,0)、
.连结AC、BC,B、C两点的坐标分别为B(1,0)、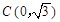 ,且当x=-10和x=8时函数的值
,且当x=-10和x=8时函数的值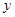 相等.
相等.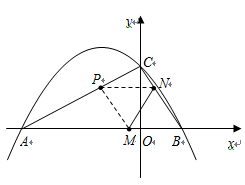
求a、b、c的值;
若点
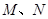 同时从
同时从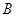 点出发,均以每秒1个单位长度的速度分别沿
点出发,均以每秒1个单位长度的速度分别沿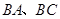 边运动,其中一个点到达终点时,另一点也随之停止运动.连结
边运动,其中一个点到达终点时,另一点也随之停止运动.连结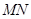 ,将
,将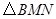 沿
沿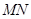 翻折,当运动时间为几秒时,
翻折,当运动时间为几秒时,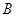 点恰好落在
点恰好落在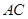 边上的
边上的 处?并求点
处?并求点 的坐标及四边形
的坐标及四边形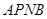 的面积;
的面积;上下平移该抛物线得到新的抛物线,设新抛物线的顶点为D,对称轴与x轴的交点为E,若△ODE与△OBC相似,求新抛物线的解析式。
某文印店,一次性复印收费 (元)与复印面数(8开纸)
(元)与复印面数(8开纸) (面)的函数关系如图所示:
(面)的函数关系如图所示:
从图象中可看出:复印超过50面的部分每面收费元,复印200面平均每面收费元;
两同学各需要复印都不多于50面的资料,他们合起来去该店复印,结果比各自独去复印两人共节省2元钱,问其中一位同学所需复印的面数不能少于多少面?