设 为平面 内的 个点,在平面 内的所有点中,若点 到点 的距离之和最小,则称点 为 的一个"中位点",例如,线段 上的任意点都是端点 的中位点,现有下列命题：
①若三个点 共线, 在线段 上,则 是 的中位点；
②直角三角形斜边的中点是该直角三角形三个顶点的中位点；
③若四个点
共线,则它们的中位点存在且唯一；
④梯形对角线的交点是该梯形四个顶点的唯一中位点．
其中的真命题是(写出所有真命题的序号)．
某空间几何体的三视图如下，则它的表面积______________.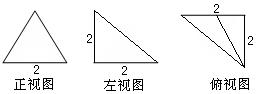
_____________.
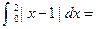下列四个命题：
①m=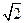
是两直线2x+my十1=0与mx+y-1=0平行的充分必要条件；②直线
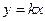与圆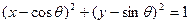
恒有公共点。③当
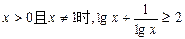；④一椭圆内切于长为6,宽为2的矩形，在矩形内随机地撒300颗黄豆，数得落在椭圆外的黄豆数为96
颗，以此实验数据为依据可以估算出椭圆的面积约为 8.16。
正确命题的序号为（写出所有正确命题的序号）
已知水平地面上有一篮球，在斜平行光线的照射下，其阴影为一椭圆（如上图），在平面直角坐标系中，O为原点，设椭圆的方程为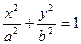
（
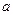
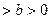），篮球与地面的接触点为H，则|OH|=.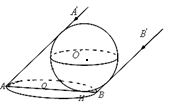
学校为了调查学生在课外读物方面的支出情况，抽取了一个容量为100的样本，其频率分布直方图如图所示，则据此估计支出在[50,60)元的同学的概率为 
