已知焦点在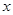 轴上的椭圆
轴上的椭圆 和双曲线
和双曲线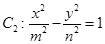 的离心率互为倒数,它们在第一象限交点的坐标为
的离心率互为倒数,它们在第一象限交点的坐标为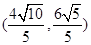 ,设直线
,设直线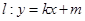 (其中
(其中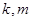 为整数).
为整数).
(1)试求椭圆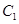 和双曲线
和双曲线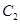 的标准方程;
的标准方程;
(2)若直线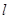 与椭圆
与椭圆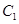 交于不同两点
交于不同两点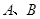 ,与双曲线
,与双曲线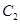 交于不同两点
交于不同两点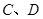 ,问是否存在直线
,问是否存在直线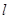 ,使得向量
,使得向量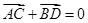 ,若存在,指出这样的直线有多少条?若不存在,请说明理由.
,若存在,指出这样的直线有多少条?若不存在,请说明理由.
已知函数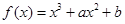 的图象上一点P(1,0),且在P点处的切线与直线
的图象上一点P(1,0),且在P点处的切线与直线 平行.
平行.
(1)求函数 的解析式;
的解析式;
(2)求函数 在区间[0,t](0<t<3)上的最大值和最小值;
在区间[0,t](0<t<3)上的最大值和最小值;
(3)在(1)的结论下,关于x的方程 在区间[1,3]上恰有两个相异的实根,求实数c的取值范围
在区间[1,3]上恰有两个相异的实根,求实数c的取值范围
厂家在产品出厂前,需对产品做检验,厂家将一批产品发给商家时,商家按合同规定也需随机抽取一定数量的产品做检验,以决定是否接收这批产品.
(1)若厂家库房中的每件产品合格的概率为0.8,从中任意取出4件进行检验,求至少有1件是合格品的概率;
(2)若厂家发给商家20件产品,其中有3件不合格.按合同规定该商家从中任取2件进行检验,只有2件都合格时才接收这批产品,否则拒收.求该商家可能检验出不合格产品数ξ的分布列及数学期望E(ξ),并求该商家拒收这批产品的概率.
给出四个等式:
1=1
1-4=-(1+2)
1-4+9=1+2+3
1-4+9-16=-(1+2+3+4)
……
(1)写出第5,6个等式,并猜测第n(n∈N*)个等式
(2)用数学归纳法证明你猜测的等式.
打鼾不仅影响别人休息,而且可能与患某种疾病有关.下表是一次调查所得的数据,(1)将本题的2*2联表格补充完整。
(2)用提示的公式计算,每一晚都打鼾与患心脏病有关吗?
提示: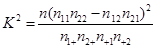
| 患心脏病 |
未患心脏病 |
合计 |
|
| 每一晚都打鼾 |
3 |
17 |
a = |
| 不打鼾 |
2 |
128 |
b = |
| 合计 |
c = |
d = |
n = |
如果复数z=(m2+m-1)+(4m2-8m+3)i (m∈R)的共轭复数对应的点在第一象限,求实数m的取值范围.