某公司生产一种电子仪器的固定成本为20000元，每生产一台仪器需增加投入100元，已知总收益函数是
其中
是仪器的产量（单位：台）：
（1）将利润
表示为产量的函数（利润
总收益
总成本）；
（2）当产量为多少台时，公司所获利润最大？最大利润是多少元？
已知函数
函数
在
处取得极值1.
（1）求实数b，c的值；
（2）求
在区间[-2，2]上的最大值．
已知圆
的圆心在坐标原点
，且恰好与直线
相切，设点A为圆上一动点，
轴于点
，且动点
满足
，设动点的轨迹为曲线
（1）求曲线C的方程，
（2）直线l与直线l，垂直且与曲线C交于B、D两点，求△OBD面积的最大值．
如图，四棱锥
中，底面
为平行四边形，
底面
（1）证明：平面
平面
;
（2）若二面角
大小为
，求
与平面
所成角的正弦值.
某市教育局为了了解高三学生体育达标情况，在某学校的高三学生体育达标成绩中随机抽取100个进行调研，按成绩分组：第l组[75，80），第2组[80，85），第3组[85，90），第4组[90，95），第5组[95，100]得到的频率分布直方图如图所示：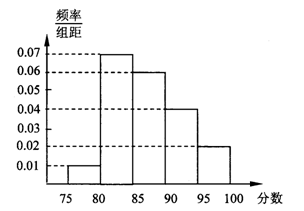
若要在成绩较高的第3，4，5组中用分层抽样抽取6名学生进行复查：
（1）已知学生甲和学生乙的成绩均在第四组，求学生甲和学生乙至少有一人被选中复查的概率；
（2）在已抽取到的6名学生中随机抽取3名学生接受篮球项目的考核，设第三组中有三名学生接受篮球项目的考核，求暑的分布列和数学期望．
已知函数
相邻两个对称轴之间的距离是
，且满足，
（1）求
的单调递减区间；
（2）在钝角△ABC中，a、b、c分别为角A、B、C的对边，sinB=
,求△ABC的面积。