设△ABC的三个内角A,B,C所对的边长分别为a,b,c.平面向量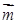 =(cosA,cosC),
=(cosA,cosC),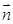 =(c,a),
=(c,a),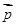 =(2b,0),且
=(2b,0),且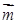 ·(
·(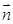 -
-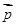 )=0
)=0
(1)求角A的大小;
(2)当|x|≤A时,求函数f(x)=sinxcosx+sinxsin(x-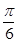 )的值域.
)的值域.
设命题p:|2x-3|<1;命题q:lg2x - (2t+l)lgx+t(t+l)≤0,
(1)若命题q所表示不等式的解集为A={x|l0≤x≤100},求实数t的值;
(2)若 p是
p是 q的必要不充分条件,求实数t的取值范围.
q的必要不充分条件,求实数t的取值范围.
己知函数f(x)=ln(x+l)-x
(1)求f(x)的单调区间;
(2)若k∈Z,且f(x-l)+x>k(1一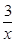 )对任意x>l恒成立,求k的最大值;
)对任意x>l恒成立,求k的最大值;
(3)对于在(0,1)中的任意一个常数a,是否存在正数x0,使得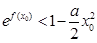 成立?请说明理由.
成立?请说明理由.
己知椭圆C: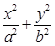 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为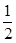 ,以原点为圆心,椭圆的短半轴为半径的圆与直线x-y+
,以原点为圆心,椭圆的短半轴为半径的圆与直线x-y+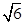 =0相切,过点P(4,0)且不垂直于x轴直线,与椭圆C相交于A、B两点.
=0相切,过点P(4,0)且不垂直于x轴直线,与椭圆C相交于A、B两点.
(1)求椭圆C的方程:
(2)求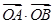 的取值范围;
的取值范围;
(3)若B点关于x轴的对称点是E,证明:直线AE与x轴相交于定点.
己知函数f(x)= +blnx+c(a>0)的图像在点(1,f(1))处的切线方程为x-y-2=0
+blnx+c(a>0)的图像在点(1,f(1))处的切线方程为x-y-2=0
(1)用a表示b,c;
(2)若函数g(x)=x-f(x)在x∈(0,1]上的最大值为2,求实数a的取值范围.