已知函数 的导函数是
的导函数是 ,
, 在
在 处取得极值,且
处取得极值,且 .
.
(Ⅰ)求 的极大值和极小值;
的极大值和极小值;
(Ⅱ)记 在闭区间
在闭区间 上的最大值为
上的最大值为 ,若对任意的
,若对任意的
 总有
总有 成立,求
成立,求 的取值范围;
的取值范围;
(Ⅲ)设 是曲线
是曲线 上的任意一点.当
上的任意一点.当 时,求直线OM斜率的最小值,据此判断
时,求直线OM斜率的最小值,据此判断 与
与 的大小关系,并说明理由.
的大小关系,并说明理由.
(本小题满分12分)设等差数列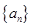 的前
的前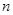 项和为
项和为 .数列
.数列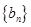 的前
的前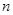 项和为
项和为 ,且
,且 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设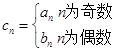 ,求数列
,求数列 的前
的前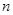 项和
项和 .
.
(本小题满分12分)在如图所示的几何体中,四边形ABCD是等腰梯形,AB//CD,∠ABC=60°,AB=2CB=2.在梯形ACEF中,EF//AC,且 平面ABCD.
平面ABCD.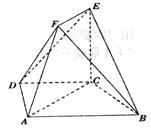
(Ⅰ)求证: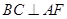 ;
;
(Ⅱ)若二面角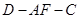 为45°,求CE的长.
为45°,求CE的长.
(本小题满分12分)已知△ABC中的三个内角A,B,C所对的边分别为 ,且满足
,且满足
(Ⅰ)求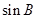 ;(Ⅱ)求△ABC的面积.
;(Ⅱ)求△ABC的面积.
(本小题满分13分)已知由非负整数组成的数列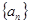 满足下列两个条件:
满足下列两个条件:
①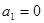 ,
,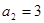 ,
,
②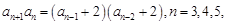
(1)求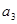 ;
;
(2)证明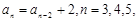 ;
;
(3)求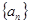 的通项公式及其前
的通项公式及其前 项和
项和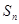 .
.
(本小题满分13分)等差数列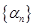 的前
的前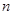 项和
项和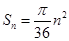 ,数列
,数列 满足
满足 .同学甲在研究性学习中发现以下六个等式均成立:
.同学甲在研究性学习中发现以下六个等式均成立:
①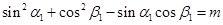 ;
;
② ;
;
③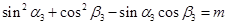 ;
;
④ ;
;
⑤ ;
;
⑥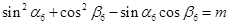 .
.
(1)求数列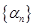 的通项公式,并从上述六个等式中选择一个,求实数
的通项公式,并从上述六个等式中选择一个,求实数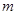 的值;
的值;
(2)根据(1)计算结果,将同学甲的发现推广为关于任意角 的三角恒等式,并证明你的结论.
的三角恒等式,并证明你的结论.