节日期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h)分成六段 


 后得到如下图的频率分布直方图.
后得到如下图的频率分布直方图.
(1)此调查公司在采样中,用到的是什么抽样方法?
(2)求这40辆小型车辆车速的众数和中位数的估计值;
(3)若从车速在 的车辆中任抽取2辆,求抽出的2辆车中车速在
的车辆中任抽取2辆,求抽出的2辆车中车速在 的车辆数
的车辆数 的分布列及数学期望.
的分布列及数学期望.
如图,三棱柱 的所有棱长都为
的所有棱长都为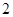 ,且
,且 平面
平面 ,
, 为
为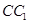 中点.
中点.
(Ⅰ)求证: 面
面 ;
;
(Ⅱ)求二面角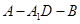 的大小的余弦值;
的大小的余弦值;
(Ⅲ)求点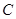 到平面
到平面 的距离.
的距离.
设椭圆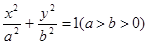 的左焦点为
的左焦点为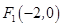 ,直线
,直线 与
与 轴交于点
轴交于点 ,过点
,过点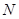 且倾斜角为30°的直线
且倾斜角为30°的直线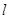 交椭圆于
交椭圆于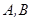 两点.
两点.
(Ⅰ)求直线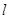 和椭圆的方程;
和椭圆的方程;
(Ⅱ)求证:点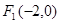 在以线段
在以线段 为直径的圆上;
为直径的圆上;
(Ⅲ)在直线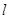 上有两个不重合的动点
上有两个不重合的动点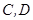 ,以
,以 为直径且过点
为直径且过点 的所有圆中,求面积最小的圆的半径长.
的所有圆中,求面积最小的圆的半径长.
已知三棱锥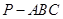 的三视图如图所示.
的三视图如图所示.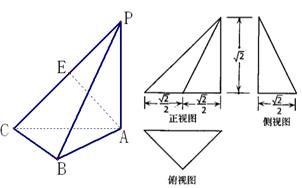
(Ⅰ)求证: 是直角三角形;
是直角三角形;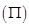 求三棱锥
求三棱锥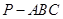 是全面积;
是全面积;
(Ⅲ)当点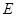 在线段
在线段 上何处时,
上何处时,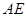 与平面
与平面 所成的角为
所成的角为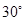 .
.
已知抛物线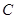 :
: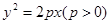 上横坐标为4的点到焦点的距离为5.
上横坐标为4的点到焦点的距离为5.
(Ⅰ)求抛物线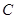 的方程;
的方程;
(Ⅱ)设直线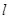 与抛物线
与抛物线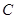 交于不同两点
交于不同两点 ,若满足
,若满足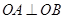 ,证明直线
,证明直线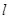 恒过定点,并求出定点
恒过定点,并求出定点 的坐标.
的坐标.
(Ⅲ)试把问题(Ⅱ)的结论推广到任意抛物线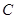 :
: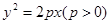 中,请写出结论,不用证明.
中,请写出结论,不用证明.
如图所示,平面 ⊥平面
⊥平面 ,
, ,
,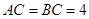 ,四边形
,四边形 是直角梯形,
是直角梯形,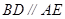 ,
,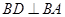 ,
, 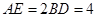 ,
, 分别为
分别为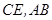 的中点.
的中点. 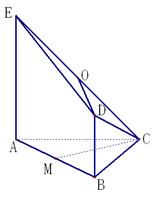
(Ⅰ) 用几何法证明: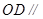 平面
平面 ;
;
(Ⅱ)用几何法证明: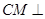 平面
平面 .
.