受日月引力的作用，海水会发生涨落，这种现象叫潮汐. 在通常情况下，船在海水涨潮时驶进航道，靠近码头，卸货后返回海洋.某港口水的深度
是时间
，单位：
的函数，记作：
，下表是该港口在某季每天水深的数据：
经过长期观察
的曲线可以近似地看做函数
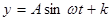的图象.
（Ⅰ）根据以上数据，求出函数的近似表达式；
（Ⅱ）一般情况下，船舶航行时船底离海底的距离为
以上时认为是安全的（船舶停靠时，船底只需不碰到海底即可），某船吃水深度（船底离水面的距离）为
，如果该船想在同一天内安全进出港，问它至多能在港内停留多长时间（忽略进出港所需时间）？
（本小题满分12分）某中学在高二年级开设大学先修课程《线性代数》，共有50名同学选修，其中男同学30名，女同学20名.为了对这门课程的教学效果进行评估，学校按性别采用分层抽样的方法抽取5人进行考核.
（1）求抽取的5人中男、女同学的人数；
（2）考核前，评估小组打算从抽取的5人中随机选出2名同学进行访谈，求选出的两名同学中恰有一名女同学的概率.
（本小题满分14分）已知椭圆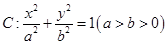
，其中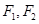
为左、右焦点，O为坐标原点.直线l与椭圆交于
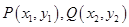两个不同点.当直线l过椭圆C右焦点F2且倾斜角为
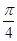时，原点O到直线l的距离为
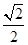.又椭圆上的点到焦点F2的最近距离为
.
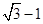（1）求椭圆C的方程；
（2）以OP，OQ为邻边做平行四边形OQNP，当平行四边形OQNP面积为
时，求平行四边形OQNP的对角线之积
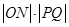的最大值；
（3）若抛物线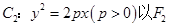
为焦点，在抛物线C2上任取一点S（S不是原点O），以OS为直径作圆，交抛物线C2于另一点R，求该圆面积最小时点S的坐标.
（本小题满分13分）已知函数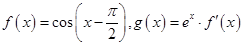
，其中e为自然对数的底数.
（1）求曲线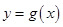
在点
处的切线方程；
（2）若对任意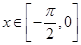
，不等式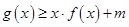
恒成立，求实数m的取值范围；
（3）试探究当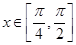
时，方程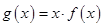
的解的个数，并说明理由.
（本小题满分12分）已知数列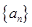
中，
（1）求证：数列
是等比数列；
（2）若
是数列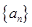的前n项和，求满足
的所有正整数n.
（本小题满分12分）学校为测评班级学生对任课教师的满意度，采用“100分制”打分的方式来计分.现从某班学生中随机抽取10名，以下茎叶图记录了他们对某教师的满意度分数（以十位数字为茎，个位数字为叶）：规定若满意度不低于98分，测评价该教师为“优秀”.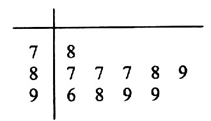
（1）求从这10人中随机选取3人，至多有1人评价该教师是“优秀”的概率；
（2）以这10人的样本数据来估计整个班级的总体数据，若从该班任选3人，记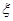
表示抽到评价该教师为“优秀”的人数，求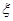的分布列及数学期望.