甲乙两地相距SKm,汽车从甲地匀速行驶到乙地,速度不得超过CKm/h,已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成; 可变部分与速度V(Km/h)的平方成正比比例系数为b, 固定成本为a.
(1)把全程运输成本y(元)表示为速度V(km/h)的函数, 并指出这个函数的定义域;
(2)为了使全程运输成本最小; 汽车应以多大的速度行驶.
某公司生产一种产品,每年需投入固定成本0.5万元,此外每生产1百件这样的产品,还需增加投入0.25万元,经市场调查知这种产品年需求量为5百件,产品销售数量为t(百件)时,销售所得的收入为( )万元。
)万元。
(1)该公司这种产品的年生产量为 百件,生产并销售这种产品得到的利润为当年产量
百件,生产并销售这种产品得到的利润为当年产量 的函数
的函数 ,求
,求 ;
;
(2)当该公司的年产量为多大时当年所获得的利润最大。
已知极坐标系的极点在直角坐标系的原点,极轴与x轴的正半轴重合.已知直线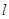 的参数方程为
的参数方程为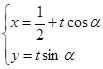
 ,曲线
,曲线 的极坐标方程为
的极坐标方程为 .
.
(1)曲线 的直角坐标方程;
的直角坐标方程;
(2)设直线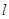 与曲线
与曲线 相交于A,B两点,当
相交于A,B两点,当 变化时,求
变化时,求 的最小值。
的最小值。
已知不等式 .
.
(1)若 ,求不等式的解集;
,求不等式的解集;
(2)若已知不等式的解集不是空集,求 的取值范围。
的取值范围。
已知函数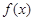 是定义在
是定义在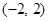 上的奇函数且是减函数,若
上的奇函数且是减函数,若 ,求实数
,求实数 的取值范围。
的取值范围。
已知f(x)=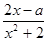 (x∈R)在区间[-1,1]上是增函数.
(x∈R)在区间[-1,1]上是增函数.
(1)求实数a的值组成的集合A;
(2)设关于x的方程f(x)=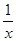 的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.
的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.