已知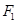 、
、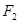 是椭圆
是椭圆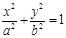
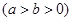 的左、右焦点,且离心率
的左、右焦点,且离心率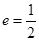 ,点
,点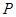 为椭圆上的一个动点,
为椭圆上的一个动点, 的内切圆面积的最大值为
的内切圆面积的最大值为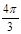 .
.
(1) 求椭圆的方程;
(2) 若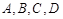 是椭圆上不重合的四个点,满足向量
是椭圆上不重合的四个点,满足向量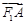 与
与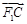 共线,
共线,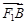 与
与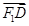 共
共
线,且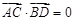 ,求
,求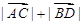 的取值范围.
的取值范围.
(本题12分) 设函数 .
.
(1) 求函数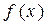 的单调区间;
的单调区间;
(2) 若函数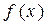 在区间(0,2)上单调递减,试求实数
在区间(0,2)上单调递减,试求实数 的取值范围;
的取值范围;
(3) 若函数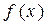 的极小值大于0,试求实数
的极小值大于0,试求实数 的取值范围.
的取值范围.
(本题12分)口袋里放了12个大小完全一样的小球,其中3个是红色的,
4个是白色的,5个是蓝色的,现从袋中任意取出4个小球,求:
(1) 取出的小球的颜色至少是两种的概率;
(2) 取出的小球的颜色是三种的概率.
(本题12分)七个人排成两排照相,前排3人,后排4人.
(1) 求甲在前排,乙在后排的概率;
(2)求甲、乙在同一排且相邻的概率;
(3) 求甲、乙之间恰好有一人的概率.
(本题12分)已知 是定义在R上的函数, 且
是定义在R上的函数, 且 在(-1,0)和(4,5)上有相同的单调性,在(0,2)和(4,5)上
在(-1,0)和(4,5)上有相同的单调性,在(0,2)和(4,5)上
有相反的单调性.
(1) 求 的值;
的值;
(2) 在函数 的图象上是否存在一点
的图象上是否存在一点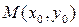 ,使得
,使得 在点
在点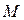 的
的
切线斜率为 ?若存在,求出点
?若存在,求出点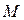 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
设函数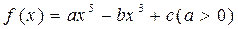 .
.
(1)若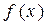 在
在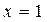 和
和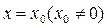 处有不同的极值,且极大值为4,
处有不同的极值,且极大值为4,
极小值为1,求 及实数
及实数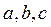 的值;
的值;
(2) 若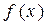 在
在 上单调递增且
上单调递增且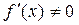 ,求
,求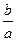 的最大值.
的最大值.