如图, 在三棱锥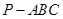 中,
中, .
.
(1)求证:平面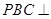 平面
平面 ;
;
(2)若 ,
,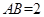 ,当三棱锥
,当三棱锥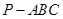 的体积最大时,求
的体积最大时,求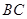 的长.
的长.
(本小题满分12分)已知函数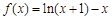 .
.
(Ⅰ)求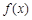 的最大值;
的最大值;
(Ⅱ)设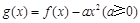 ,
,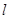 是曲线
是曲线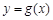 的一条切线,证明:曲线
的一条切线,证明:曲线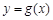 上的任意一点都不可能在直线
上的任意一点都不可能在直线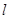 的上方;
的上方;
(Ⅲ)求证: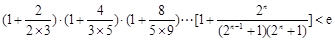 (其中e为自然对数的底数,n∈N*).
(其中e为自然对数的底数,n∈N*).
(本小题满分12分)如图所示,抛物线C1:x2=4y在点A,B处的切线垂直相交于点P,直线AB与椭圆,C2: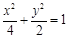 相交于C,D两点.
相交于C,D两点.
(Ⅰ)求抛物线C1的焦点F与椭圆C2的左焦点F1的距离;
(Ⅱ)设点P到直线AB的距离为d,是否存在直线AB,使得|AB|,d,|CD|成等比数列?若存在,求出直线AB的方程;若不存在,请说明理由.
(本小题满分12分)现有6名学生,按下列要求回答问题(列出算式,并计算出结果):
(Ⅰ)6人站成一排,甲站在乙的前面(甲、乙可以不相邻)的不同站法种数;
(Ⅱ)6人站成一排,甲、乙相邻,且丙与乙不相邻的不同站法种数;
(Ⅲ)把这6名学生全部分到4个不同的班级,每个班级至少1人的不同分配方法种数;
(Ⅳ)6人站成一排,求在甲、乙相邻条件下,丙、丁不相邻的概率.
(本小题满分12分)如图,四棱锥P—ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD=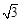 ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动.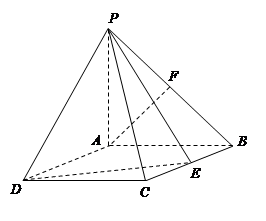
(Ⅰ)证明:无论点E在边BC的何处,都有PE⊥AF;
(Ⅱ)当BE为何值时,PA与平面PDE所成角的大小是45°?
(本小题满分12分)已知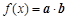 ,其中
,其中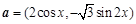 ,
,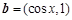 ,
,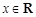 .
.
(Ⅰ)求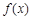 的单调递减区间;
的单调递减区间;
(Ⅱ)在△ABC中,角A,B,C所对的边分别为a,b,c,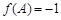 ,
,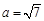 ,且向量
,且向量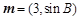 与
与 共线,求边长b和c的值.
共线,求边长b和c的值.