经过点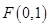 且与直线
且与直线 相切的动圆的圆心轨迹为
相切的动圆的圆心轨迹为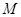 .点
.点 、
、 在轨迹
在轨迹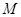 上,且关于
上,且关于 轴对称,过线段
轴对称,过线段 (两端点除外)上的任意一点作直线
(两端点除外)上的任意一点作直线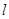 ,使直线
,使直线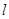 与轨迹
与轨迹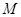 在点
在点 处的切线平行,设直线
处的切线平行,设直线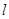 与轨迹
与轨迹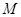 交于点
交于点 、
、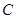 .
.
(1)求轨迹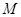 的方程;
的方程;
(2)证明: ;
;
(3)若点 到直线
到直线 的距离等于
的距离等于 ,且△
,且△ 的面积为20,求直线
的面积为20,求直线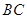 的方程.
的方程.
已知向量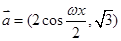 ,
, ,
, ,设函数
,设函数 的部分图象如图所示,A为图象的最低点,B,C为图象与x轴的交点,且
的部分图象如图所示,A为图象的最低点,B,C为图象与x轴的交点,且 为等边三角形,其高为
为等边三角形,其高为 .
.
(1)求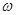 的值及函数
的值及函数 的值域;
的值域;
(2)若 ,且
,且 ,求
,求 的值.
的值.
在直角坐标平面内,直线l过点P(1,1),且倾斜角α= .以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,已知圆C的极坐标方程为ρ=4sinθ.
.以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,已知圆C的极坐标方程为ρ=4sinθ.
(1)求圆C的直角坐标方程;
(2)设直线l与圆C交于A、B两点,求|PA|·|PB|的值.
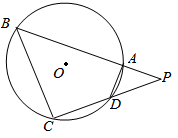
如图,四边形ABCD是圆 的内接四边形,延长BA和CD相交于点P,
的内接四边形,延长BA和CD相交于点P, ,
, .
.
(Ⅰ)求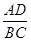 的值;
的值;
(Ⅱ)若BD为圆 的直径,且
的直径,且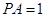 ,求BC的长.
,求BC的长.
设函数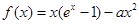 .
.
(1)若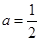 ,求的单调区间;
,求的单调区间;
(2)若当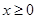 时,
时,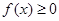 ,求
,求 的取值范围.
的取值范围.
已知定点F(3,0)和动点P(x,y),H为PF的中点,O为坐标原点,且满足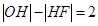 .
.
(1)求点P的轨迹方程;
(2)过点F作直线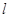 与点P的轨迹交于A,B两点,点C(2,0).连接AC,BC与直线
与点P的轨迹交于A,B两点,点C(2,0).连接AC,BC与直线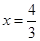 分别交于点M,N.试证明:以MN为直径的圆恒过点F.
分别交于点M,N.试证明:以MN为直径的圆恒过点F.