已知定点F(3,0)和动点P(x,y),H为PF的中点,O为坐标原点,且满足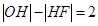 .
.
(1)求点P的轨迹方程;
(2)过点F作直线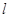 与点P的轨迹交于A,B两点,点C(2,0).连接AC,BC与直线
与点P的轨迹交于A,B两点,点C(2,0).连接AC,BC与直线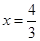 分别交于点M,N.试证明:以MN为直径的圆恒过点F.
分别交于点M,N.试证明:以MN为直径的圆恒过点F.
心理学家分析发现视觉和空间能力与性别有关, 某数学兴趣小组为了验证这个结论,从兴趣小组中按分层抽样的方法抽取50名同学 (男30女20), 给所有同学几何题和代数题各一题, 让各位同学自由选择一道题进行解答.选题情况如下表:(单位: 人)
(Ⅰ)能否据此判断有97.5%的把握认为视觉和空间能力与性别有关?
(Ⅱ)经过多次测试后, 甲每次解答一道几何题所用的时间在5—7分钟, 乙每次解答一道几何题所用的时间在6—8分钟, 现甲、 乙各解同一道几何题, 求乙比甲先解答完的概率.
(Ⅲ)现从选择做几何题的8名女生中任意抽取两人对她们的答题情况进行全程研究,记甲、 乙两女生被抽到的人数为X, 求X的分布列及数学期望E (X).
附表及公式
如图, 在直三棱柱 ABC - A1B1C1中, D、 E分别是BC和CC1的中点, 已知AB=AC=AA1=4,∠BAC=90°.
(Ⅰ)求证: B1D⊥平面AED;
(Ⅱ)求二面角B1-AE-D的余弦值;
(Ⅲ)求三棱锥A-B1DE的体积.
已知数列{an}的前n项和为Sn, 且满足a1 = 2, nan + 1 = Sn + n(n + 1).
(Ⅰ)求数列{an}的通项公式an;
(Ⅱ)设Tn为数列 }的前n项和, 求Tn;
}的前n项和, 求Tn;
(Ⅲ)设 , 证明:
, 证明:
选修4-5: 不等式选讲
已知函数 f (x)=" |x" - 2|,g(x)=" -|x" + 3| +m.
(Ⅰ)若关于x的不等式 g(x)≥0的解集为 [-5, -1], 求实数m的值;
(Ⅱ)若 f (x)的图象恒在 g(x)图象的上方, 求实数m的取值范围.
选修4-4: 坐标系与参数方程
在极坐标系中, 已知圆C的圆心C( ), 半径r =
), 半径r = .
.
(Ⅰ)求圆C的极坐标方程;
(Ⅱ)若 α ∈  , 直线
, 直线 的参数方程为
的参数方程为 为参数), 直线
为参数), 直线 交圆C于A、 B两点, 求弦长|AB|的取值范围.
交圆C于A、 B两点, 求弦长|AB|的取值范围.