设函数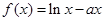 .
.
(Ⅰ)求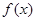 的单调区间;
的单调区间;
(Ⅱ)若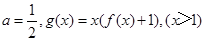 ,且
,且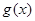 在区间
在区间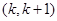 内存在极值,求整数
内存在极值,求整数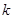 的值.
的值.
从某校高一年级的1 002名新生中用系统抽样的方法抽取一个容量为100的身高样本,数据如下:(单位:cm)
| 168 |
165 |
171 |
167 |
170 |
165 |
170 |
152 |
175 |
174 |
| 165 |
170 |
168 |
169 |
171 |
166 |
164 |
155 |
164 |
158 |
| 170 |
155 |
166 |
158 |
155 |
160 |
160 |
164 |
156 |
162 |
| 160 |
170 |
168 |
164 |
174 |
171 |
165 |
179 |
163 |
172 |
| 180 |
174 |
173 |
159 |
163 |
172 |
167 |
160 |
164 |
169 |
| 151 |
168 |
159 |
168 |
176 |
155 |
165 |
165 |
169 |
162 |
| 177 |
158 |
175 |
165 |
169 |
151 |
163 |
166 |
163 |
167 |
| 178 |
165 |
158 |
170 |
169 |
159 |
155 |
163 |
153 |
155 |
| 167 |
163 |
164 |
158 |
168 |
167 |
161 |
162 |
167 |
158 |
| 161 |
165 |
174 |
156 |
167 |
166 |
162 |
161 |
164 |
166 |
(1)试作出该样本的频率分布表;
(2)画出频率分布直方图;
(3)估计总体中
身高小于160 cm的频率.
(1)为了调查某班学生的身高情况,利用系统抽样的方法,样本容量为40.这个班共分5个组,每个组都有8名学生,他们的座次是按照个子高矮进行编排的.小王是这样做的,抽样距是8,按照每个小组的座次顺序进行编号,你觉得这样抽取的样本具有代表性吗?
(2)为了调查某路口一个月的交通流量情况,小刘采用系统抽样的方法,样本距为7,从每周中随机抽取一天,他正好抽取的是星期一,这样他每个星期一对这个路口的交通流量进行了统计,最后做出调查报告.你认为小刘这样的抽样方法有什么问题?应当怎样改进?
某私立学校共有员工160人,其中有任课教师120人,管理人员16人,后勤服务人员24人,为了了解员工的某种情况,要从中抽取一个容量为20的样本.用分层抽样方法抽取样本,写出过程.
如果样本点只有两个(x1,y1)、(x2,y2),那么用最小二乘法估计得到的直线与用两点式求出的直线方程一致吗?试给出证明.
两个具有线性相关关系的变量的一组数据为:
| 数据 |
1 |
2 |
3 |
… |
n |
| 变量x |
x1 |
x2 |
x3 |
… |
xn |
| 变量y |
y1 |
y2 |
y3 |
… |
yn |
将以上数据,以x为自变量,y为因变量,得回归方程为 =bx+a;将y为自变量,x为因变量,得回归方程为
=bx+a;将y为自变量,x为因变量,得回归方程为 =b′y+a′.
=b′y+a′.
定义两个变量的相关关系数r的计算公式为r= ,它可表示两个变量线性关系的强弱.
,它可表示两个变量线性关系的强弱.
试问r能否用上述两方程中的b,a与b′,a′表示?如能,怎样表示?