一个袋中装有四个形状大小完全相同的球，球的编号分别为1，2，3，4.
(Ⅰ)从袋中随机抽取两个球，求取出的球的编号之和不大于4的概率；
(Ⅱ)先从袋中随机取一个球，该球的编号为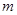
，将球放回袋中，然后再从袋中随机取一个球，该球的编号为
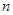，求
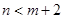的概率．
将并排的有不同编号的5个房间安排给5个工作人员临时休息，假定每个人可以选择任一房间，且选择各个房间是等可能的，求恰有2个房间无人选择且这2个房间不相邻的安排方式的种数．
有3名男生，4名女生，在下列不同要求下，求不同的排列方法总数：
(1)选其中5人排成一排；
(2)排成前后两排，前排3人，后排4人；
(3)全体排成一排，甲不站在排头也不站在排尾；
(4)全体排成一排，女生必须站在一起；
(5)全体排成一排，男生互不相邻；
(6)全体排成一排，甲、乙两人中间恰好有3人．
某工程队有6项工程需要先后单独完成，其中工程乙必须在工程甲完成后才能进行，工程丙必须在工程乙完成后才能进行，又工程丁必须在工程丙完成后立即进行．求安排这6项工程的不同排法种数．
用0,1,3,5,7五个数字，可以组成多少个没有重复数字且5不在十位上的五位数？
某区有7条南北向街道，5条东西向街道(如图)．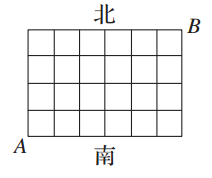
(1)图中共有多少个矩形？
(2)从A点走向B点最短的走法有多少种？