如图,四边形 是正方形,
是正方形, ,
,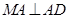 ,
,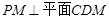 ,
, 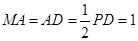
(Ⅰ)求证:平面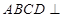 平面
平面 ;
;
(Ⅱ)求三棱锥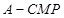 的高
的高 
在四棱锥P-ABCD中,侧面PAD丄底面ABCD,侧 棱PA="PD" =
棱PA="PD" = ,底面 ABCD为直角梯形,其中BC//AD,AB丄AD,AD=2AB=2BC=2,0为AD中点.
,底面 ABCD为直角梯形,其中BC//AD,AB丄AD,AD=2AB=2BC=2,0为AD中点.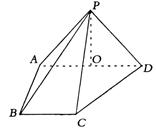
①求证PO丄平面ABCD
②求异面直线PB与CD的夹角;
③求点A到平面 PCD的距离.
PCD的距离.
用红、黄、蓝、白、橙五种不同颜色的鲜花布置如图所示的花圃(不一定用完每一种颜色的鲜花),要求同一区域上用同一种颜色的鲜花,相邻区域用不同颜色的鲜花.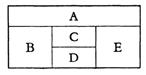
①求恰 有两个区域用红色鲜花的概率;
有两个区域用红色鲜花的概率;
②记花圃中红色鲜花区域的块数为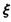 求
求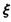 的分布列和数
的分布列和数 学期望E
学期望E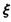
已知函数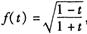 h
h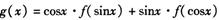 ,
,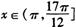
①将函数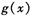 化简成
化简成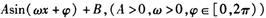 的形式.
的形式.
②求函数 的值域.
的值域.
(本小题满分12分)
已知 ,
,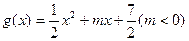 ,直线
,直线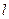 与函数
与函数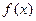 、
、 的图象都相切,且与函数
的图象都相切,且与函数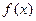 的图象的切点的横坐标为
的图象的切点的横坐标为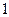 .
.
(Ⅰ)求直线 的方程及
的方程及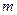 的值;
的值;
(Ⅱ)若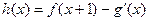 (其中
(其中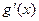 是
是 的导函数),求函数
的导函数),求函数
 的最大值;
的最大值;
(Ⅲ)当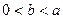 时,求证:
时,求证:
(本小题满分12分)
甲方是一农场,乙方是一工厂,由于乙方生产须占用甲方的资源,因此甲方有权向乙方索赔以弥补经济损失并获得一定净收入,在乙方不赔付的情况下,乙方的年利润x(元)与年产量t(吨)满足函数关系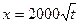 。若乙方每生产一吨产品必须赔付甲方s元(以下称s为赔付价格)。
。若乙方每生产一吨产品必须赔付甲方s元(以下称s为赔付价格)。
(1)将乙方的年利润w(元)表示为年产量t(吨)的函数,并求出乙方获得最 大利润的年产量;
大利润的年产量;
(2)甲方每年受乙方生产影响的经济损失金额y=0. 002t2(元),在乙方按照获得最大利润的产量进行生产的前提下,甲方要在索赔中获得最大净收入,应向乙方要求的赔付价格s是多少?
002t2(元),在乙方按照获得最大利润的产量进行生产的前提下,甲方要在索赔中获得最大净收入,应向乙方要求的赔付价格s是多少?