如图1,在四棱锥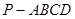 中,
中,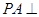 底面
底面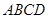 ,面
,面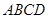 为正方形,
为正方形,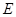 为侧棱
为侧棱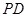 上一点,
上一点,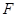 为
为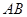 上一点.该四棱锥的正(主)视图和侧(左)视图如图2所示.
上一点.该四棱锥的正(主)视图和侧(左)视图如图2所示.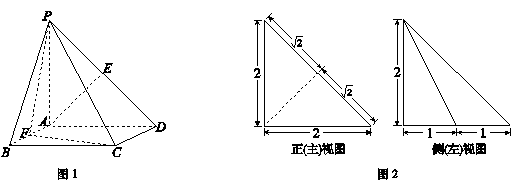
(Ⅰ)求四面体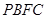 的体积;
的体积;
(Ⅱ)证明: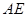 ∥平面
∥平面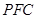 ;
;
(Ⅲ)证明:平面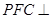 平面
平面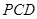 .
.
甲、乙、丙三人轮流投掷一枚质地均匀的正方体骰子,规则如下:如果某人某一次掷出1点,则下一次继续由此人掷,如果掷出其他点数,则另外两个人抓阄决定由谁来投掷,且第一次由甲投掷。 设第n次由甲投掷的概率是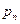 ,由乙或丙投掷的概率均为
,由乙或丙投掷的概率均为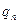 .
.
(1)计算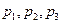 的值;
的值;
(2)求数列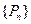 的通项公式;
的通项公式;
(3)如果一次投掷中,由任何两个人投掷的概率之差的绝对值小于0.001,则称此次投掷是“机会接近均等”,那么从第几次投掷开始,机会接近均等?
随机抽取某厂的某种产品200件,经质检,其中有一等品126件、二等品50件、三等品20件、次品4件.已知生产1件一、二、三等品获得的利润分别为6万元、2万元、1万元,而1件次品亏损2万元.设1件产品的利润(单位:万元)为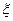 .
.
(1)求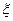 的分布列;
的分布列;
(2)求1件产品的平均利润(即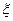 的数学期望);
的数学期望);
(3)经技术革新后,仍有四个等级的产品,但次品率降为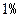 ,一等品率提高为
,一等品率提高为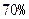 .如果此时要求1件产品的平均利润不小于4.73万元,则三等品率最多是多少?
.如果此时要求1件产品的平均利润不小于4.73万元,则三等品率最多是多少?
求由曲线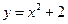 与
与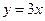 ,
,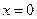 ,
,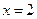 所围成的平面图形的面积(画出图形)。
所围成的平面图形的面积(画出图形)。
已知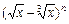 的二项展开式中所有奇数项的系数之和为512,
的二项展开式中所有奇数项的系数之和为512,
(1)求展开式的所有有理项.
(2)求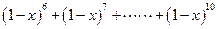 展开式中
展开式中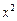 项的系数.
项的系数.
在极坐标系中,已知圆ρ=2cosθ与直线3ρcosθ+4ρsinθ+a=0相切,求实数a的值。