如图1，在平面直角坐标系中，正方形OABC的顶点A（﹣6，0），过点E（﹣2，0）作EF∥AB，交BO于F；
（1）求EF的长；
（2）过点F作直线l分别与直线AO、直线BC交于点H、G；
①根据上述语句，在图1上画出图形，并证明
；
②过点G作直线GD∥AB，交x轴于点D，以圆O为圆心，OH长为半径在x轴上方作半圆（包括直径两端点），使它与GD有公共点P．如图2所示，当直线l绕点F旋转时，点P也随之运动，证明：
，并通过操作、观察，直接写出BG长度的取值范围（不必说理）；
（3）在（2）中，若点M（2，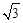
），探索2PO+PM的最小值．
如图，C是线段AB的中点，D是线段BC的中点，已知图中所有线段的长度之和为39，求线段BC的长.
一种蔬菜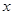
千克，不加工直接出售每千克可卖
元；如果经过加工质量减少了
，价格增加了
，
问：（1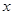）千克这种蔬菜加工后可卖多少钱；
（2）如果这种蔬菜1 000千克，不加工直接出售每千克可卖1.50元，问加工后原1 000千克这种蔬菜可卖多少钱？比加工前多卖多少钱？
用同样大小的黑色棋子按如图所示的规律摆放：
（1）第5个图形有多少颗黑色棋子？
（2）第几个图形有2 013颗黑色棋子？请说明理由．
一个两位数，把它十位上的数字与个位数字对调，得到一个新的两位数.试说明原来的两位数与新两位数的差一定能被9整除.
化简关于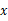
的代数式
.当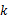
为何值时，代数式的值是常数？