如图，抛物线y﹣x24与x轴交于A、B两点，与y轴交于C点，-优题课

如图，抛物线y=﹣x²+4与x轴交于A、B两点，与y轴交于C点，点P是抛物线上的一个动点且在第一象限，过点P作x轴的垂线，垂足为D，交直线BC于点E．

（1）求点A、B、C的坐标和直线BC的解析式；
（2）求△ODE面积的最大值及相应的点E的坐标；
（3）是否存在以点P、O、D为顶点的三角形与△OAC相似？若存在，请求出点P的坐标，若不存在，请说明理由．

科目数学题型解答题难度较难

知识点：二次函数在给定区间上的最值

如图，在 $ΔABC$ 中， $∠ C = 90 °$ ， $AC = 3$ ， $BC = 4$ ， $P$ 为 $BC$ 边上的动点（与 $B$ 、 $C$ 不重合）， $PD / / AB$ ，交 $AC$ 于点 $D$ ，连接 $AP$ ，设 $CP = x$ ， $ΔADP$ 的面积为 $S$ ．

（1）用含 $x$ 的代数式表示 $AD$ 的长；

（2）求 $S$ 与 $x$ 的函数表达式，并求当 $S$ 随 $x$ 增大而减小时 $x$ 的取值范围．

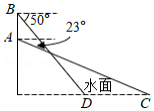
我市在凤城河风景区举办了端午节赛龙舟活动，小亮在河畔的一幢楼上看到一艘龙舟迎面驶来，他在高出水面 $15 m$ 的 $A$ 处测得在 $C$ 处的龙舟俯角为 $23 °$ ；他登高 $6 m$ 到正上方的 $B$ 处测得驶至 $D$ 处的龙舟俯角为 $50 °$ ，问两次观测期间龙舟前进了多少？（结果精确到 $1 m$ ，参考数据： $\tan 23 ° \approx 0.42$ ， $\tan 40 ° \approx 0.84$ ， $\tan 50 ° \approx 1.19$ ， $\tan 67 ° \approx 2.36)$

如图，已知线段 $a$ ，点 $A$ 在平面直角坐标系 $xOy$ 内．

（1）用直尺和圆规在第一象限内作出点 $P$ ，使点 $P$ 到两坐标轴的距离相等，且与点 $A$ 的距离等于 $a$ ．（保留作图痕迹，不写作法）

（2）在（1）的条件下，若 $a = 2 \sqrt{5}$ ， $A$ 点的坐标为 $(3, 1)$ ，求 $P$ 点的坐标．

近年来，我市大力发展城市快速交通，小王开车从家到单位有两条路线可选择，路线 $A$ 为全程 $25 km$ 的普通道路，路线 $B$ 包含快速通道，全程 $30 km$ ，走路线 $B$ 比走路线 $A$ 平均速度提高 $50 %$ ，时间节省 $6 \min$ ，求走路线 $B$ 的平均速度．

一只不透明袋子中装有1个白球和若干个红球，这些球除颜色外都相同，某课外学习小组做摸球试验：将球搅匀后从中任意摸出1个球，记下颜色后放回、搅匀，不断重复这个过程，获得数据如下：

摸球的次数	200	300	400	1000	1600	2000
摸到白球的频数	72	93	130	334	532	667
摸到白球的频率	0.3600	0.3100	0.3250	0.3340	0.3325	0.3335

（1）该学习小组发现，摸到白球的频率在一个常数附近摆动，这个常数是　　．（精确到 $0.01)$ ，由此估出红球有　　个．

（2）现从该袋中摸出2个球，请用树状图或列表的方法列出所有等可能的结果，并求恰好摸到1个白球，1个红球的概率．