某投资公司年初用 万元购置了一套生产设备并即刻生产产品,已知与生产产品相关的各种配套费用第一年需要支出
万元购置了一套生产设备并即刻生产产品,已知与生产产品相关的各种配套费用第一年需要支出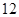 万元,第二年需要支出
万元,第二年需要支出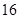 万元,第三年需要支出
万元,第三年需要支出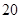 万元,……,每年都比上一年增加支出
万元,……,每年都比上一年增加支出 万元,而每年的生产收入都为
万元,而每年的生产收入都为 万元.假设这套生产设备投入使用
万元.假设这套生产设备投入使用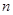 年,
年,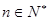 ,生产成本等于生产设备购置费与这
,生产成本等于生产设备购置费与这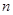 年生产产品相关的各种配套费用的和,生产总利润
年生产产品相关的各种配套费用的和,生产总利润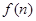 等于这
等于这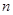 年的生产收入与生产成本的差. 请你根据这些信息解决下列问题:
年的生产收入与生产成本的差. 请你根据这些信息解决下列问题:
(Ⅰ)若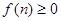 ,求
,求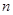 的值;
的值;
(Ⅱ)若干年后,该投资公司对这套生产设备有两个处理方案:
方案一:当年平均生产利润取得最大值时,以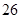 万元的价格出售该套设备;
万元的价格出售该套设备;
方案二:当生产总利润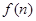 取得最大值时,以
取得最大值时,以 万元的价格出售该套设备. 你认为哪个方案更合算?请说明理由.
万元的价格出售该套设备. 你认为哪个方案更合算?请说明理由.
已知椭圆的一个顶点为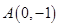 ,焦点在
,焦点在 轴上,若右焦点到直线
轴上,若右焦点到直线 的距离为3.
的距离为3.
(1)求椭圆的标准方程;
(2)设直线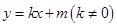 与椭圆相交于不同的两点
与椭圆相交于不同的两点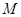 、
、 ,当
,当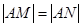 时,求
时,求 的取值范围.
的取值范围.
已知数列 的前
的前 项和是
项和是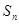 ,且
,且 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设 ,求适合方程
,求适合方程 的正整数
的正整数 的值.
的值.
如图,在三棱锥 中,
中, 底面
底面 ,
,  为
为 的中点,
的中点, .
.
(1)求证: 平面
平面 ;
;
(2)求点 到平面
到平面 的距离。
的距离。
对某校高一年级学生参加社区服务次数统计,随机抽取了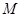 名学生作为样本,得到这
名学生作为样本,得到这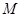 名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表如下:
名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表如下: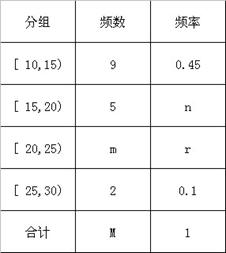
(1)求出表中 的值;
的值;
(2)在所取样本中,从参加社区服务的次数不少于 次的学生中任选
次的学生中任选 人,求至少一人参加社区服务次数在区间
人,求至少一人参加社区服务次数在区间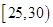 内的概率.
内的概率.
已知函数 .
.
(1)求函数 的最小正周期和最值;
的最小正周期和最值;
(2)求函数 的单调递减区间.
的单调递减区间.